题目:最长有效括号
给定一个只包含 '(' 和 ')' 的字符串,找出最长的包含有效括号的子串的长度。
示例 1:
输入: "(()"
输出: 2
解释: 最长有效括号子串为 "()"
示例 2:
输入: ")()())"
输出: 4
解释: 最长有效括号子串为 "()()"
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-valid-parentheses
解题思路
可以使用栈对下标推入/推出方式,原理如下:
- 遍历字符串,当字符为
(时把下标推入栈 - 当字符为
)时推出栈顶坐标,推出后如果栈为空,则把当前下标推入栈- 当栈为空时把当前下标推入栈是因为在有效字符串前需要有一个下标,有这个下标才能计算出有效字符长度,如下图
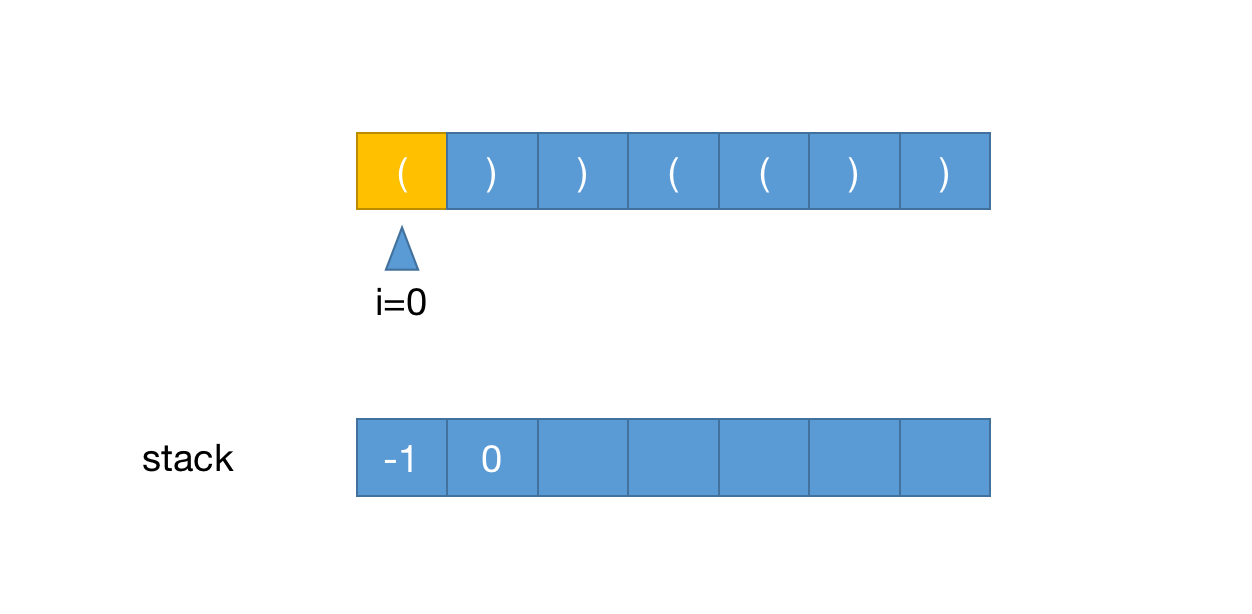
一开始要先把-1推入栈,原因如上,i=0时字符是(,把0推入栈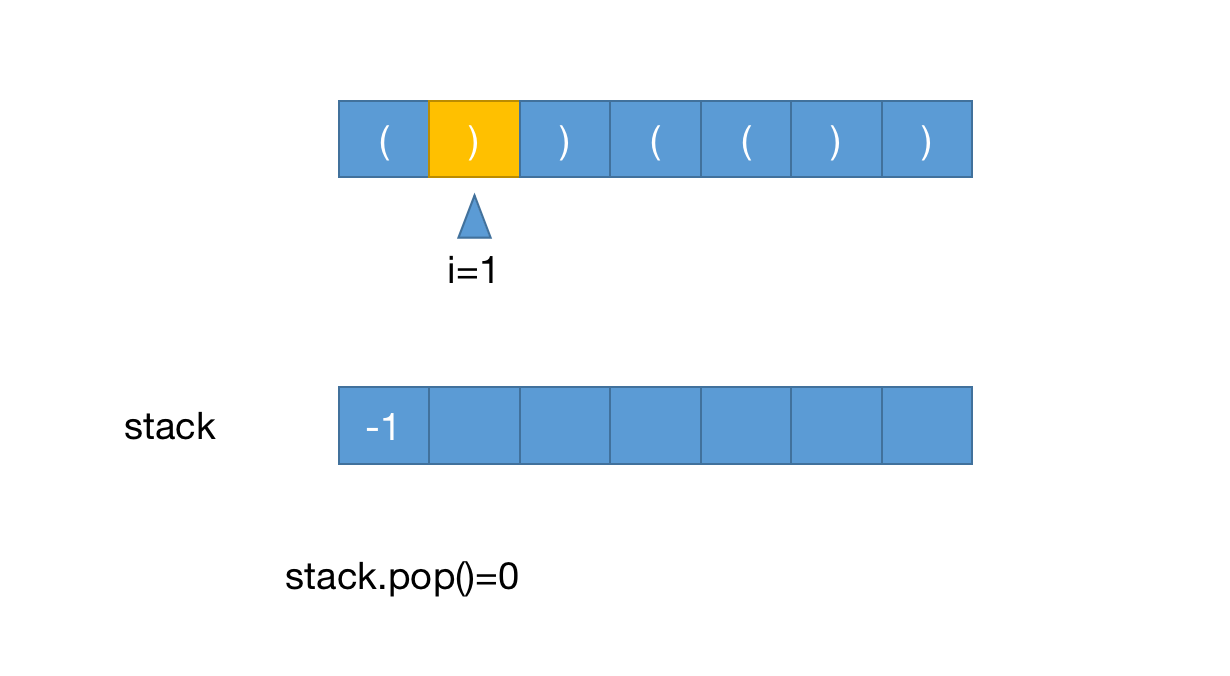
i=1时字符),栈顶推出,计算当前有效字符长度,代码为
maxLen=1-(-1)=2maxLen = i - stack[stack.length-1]
当i=2时,字符),栈顶推出,此时栈为空,为了让有效字符前始终有一个下标,把当前下标推入栈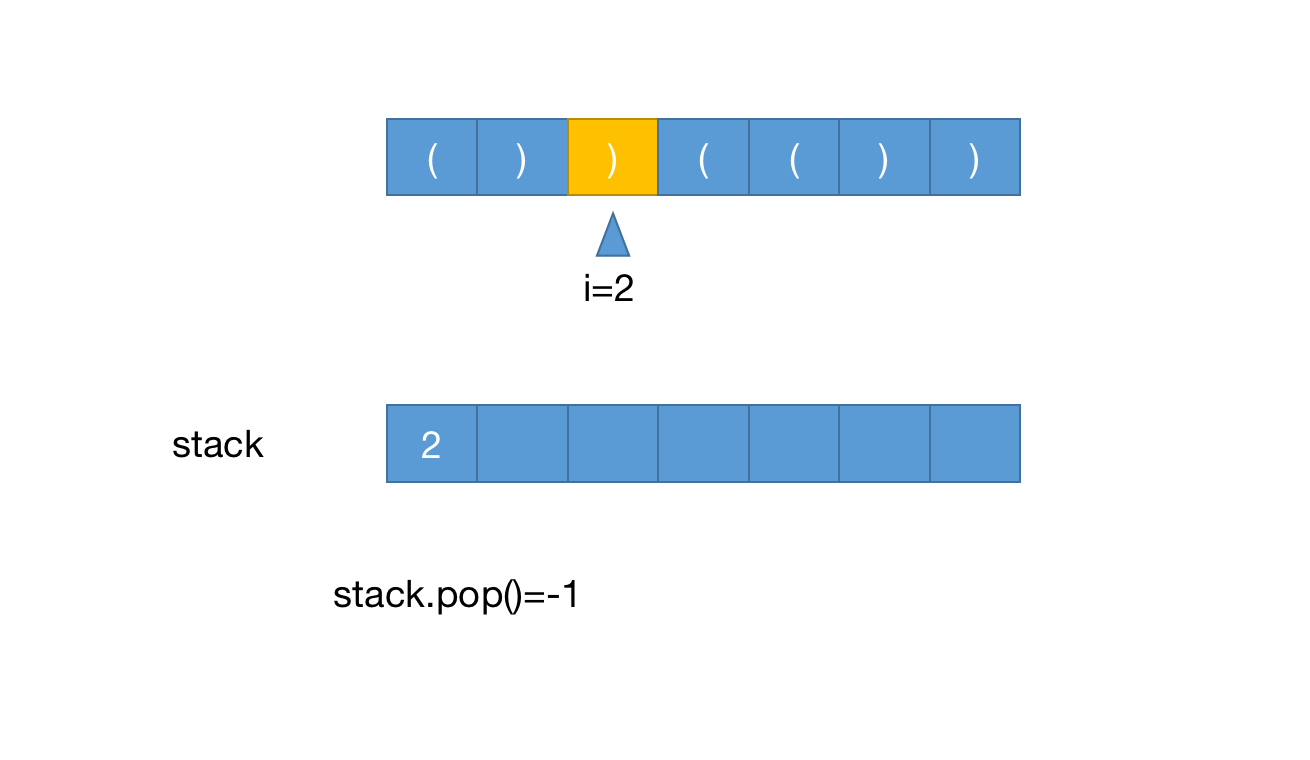
当i=3时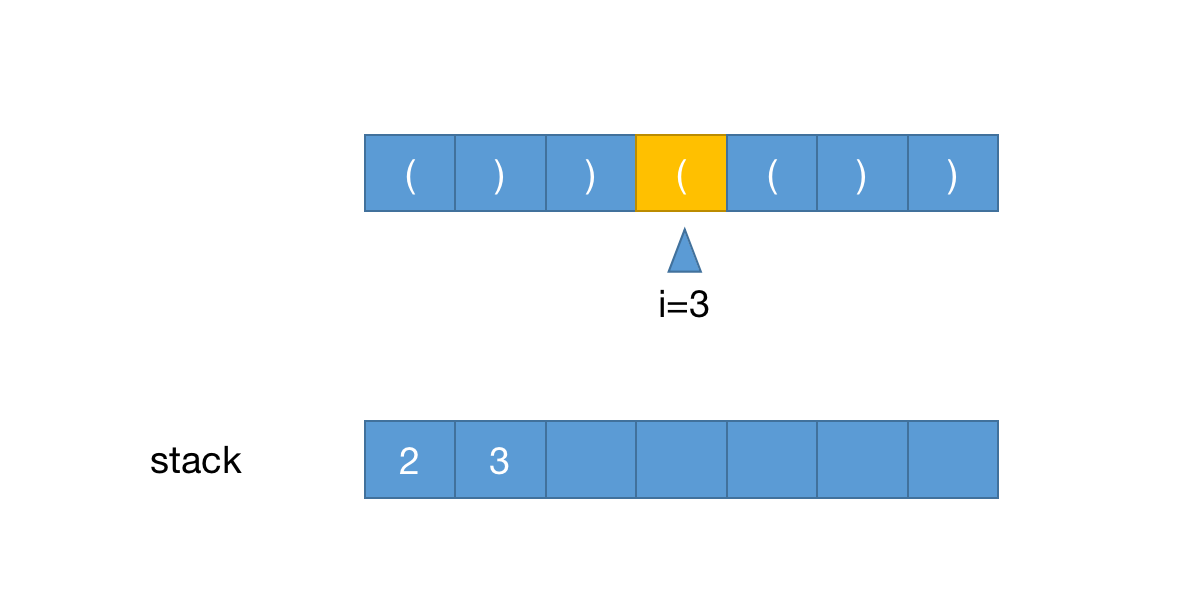
当i=4时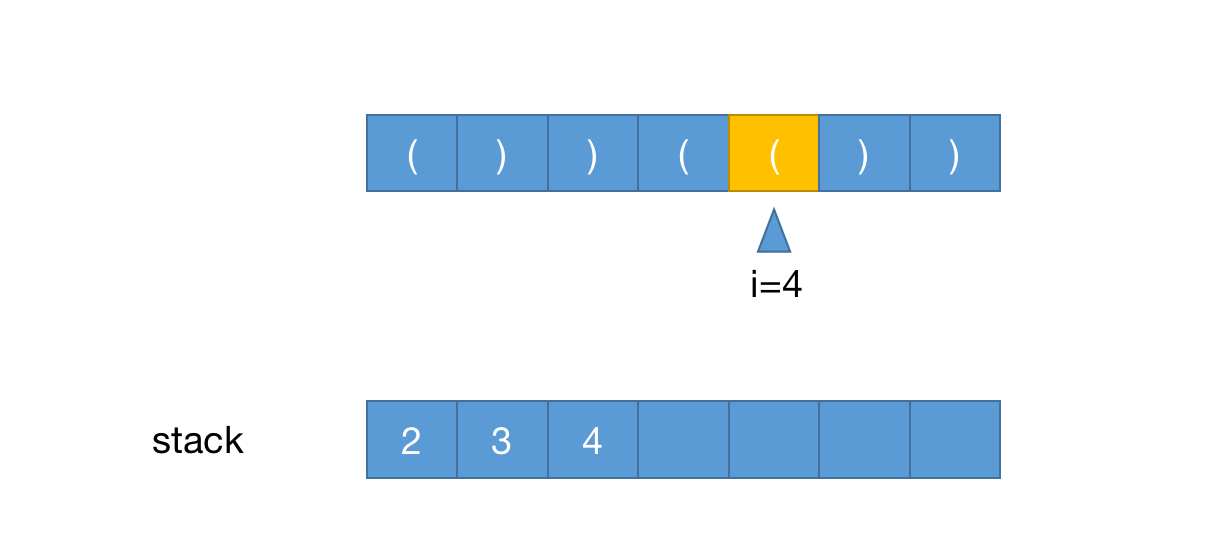
当i=5时,栈顶推出4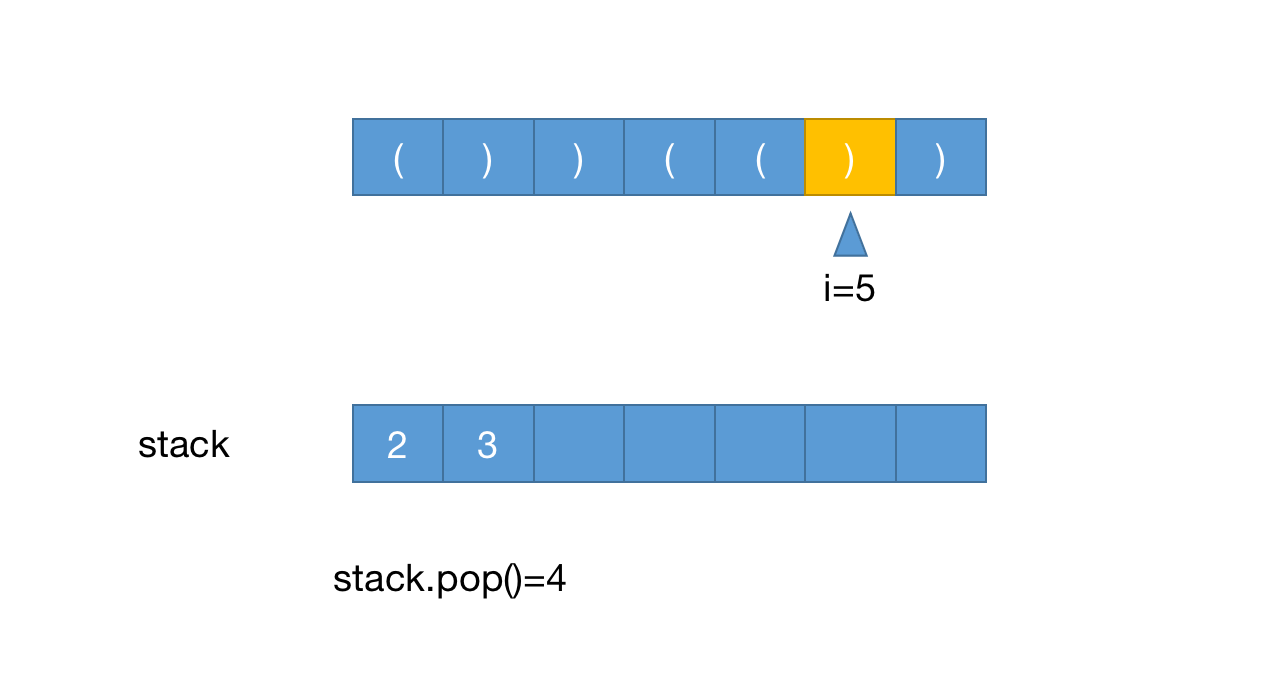
maxLen=5-3=2
当i=6时,栈顶推出3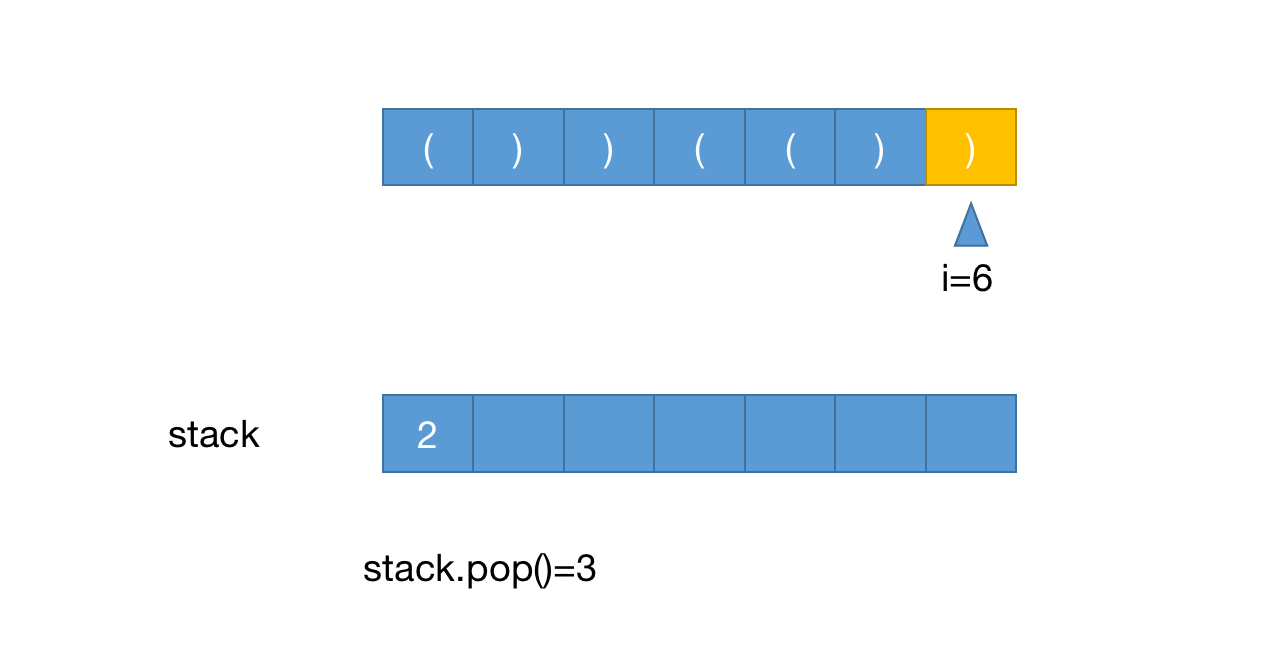
maxLen=6-2=4 - 当栈为空时把当前下标推入栈是因为在有效字符串前需要有一个下标,有这个下标才能计算出有效字符长度,如下图
代码实现
let longestValidParentheses = function (s) {
let stack = [],
maxLen = 0;
stack.push(-1);
for (let i = 0; i < s.length; i++) {
if (s[i] === '(') {
stack.push(i)
} else {
stack.pop();
if (stack.length === 0) stack.push(i);
maxLen = Math.max(maxLen, i - stack[stack.length - 1])
}
}
return maxLen
};