28.实现 strStr() | LeetCode题解

题目：实现 strStr()

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

示例 1:

输入: haystack = "hello", needle = "ll"
输出: 2

示例 2:

输入: haystack = "aaaaa", needle = "bba"
输出: -1

说明:

当needle是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当needle是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/implement-strstr

解题思路

字符串匹配算法比较经典的有KMP、BM、BF以及Sunday，在了解这些算法前要先知道这些算法诞生的原因是什么。

一般来说做字符串匹配最容易解决的办法就是暴力解决法，暴力解决的思路就是每个字符进行对比，如果遇到不相等的字符，那么长度较短的字符串就向后退一位重新开始匹配。以下面的图为举一个简单的例子
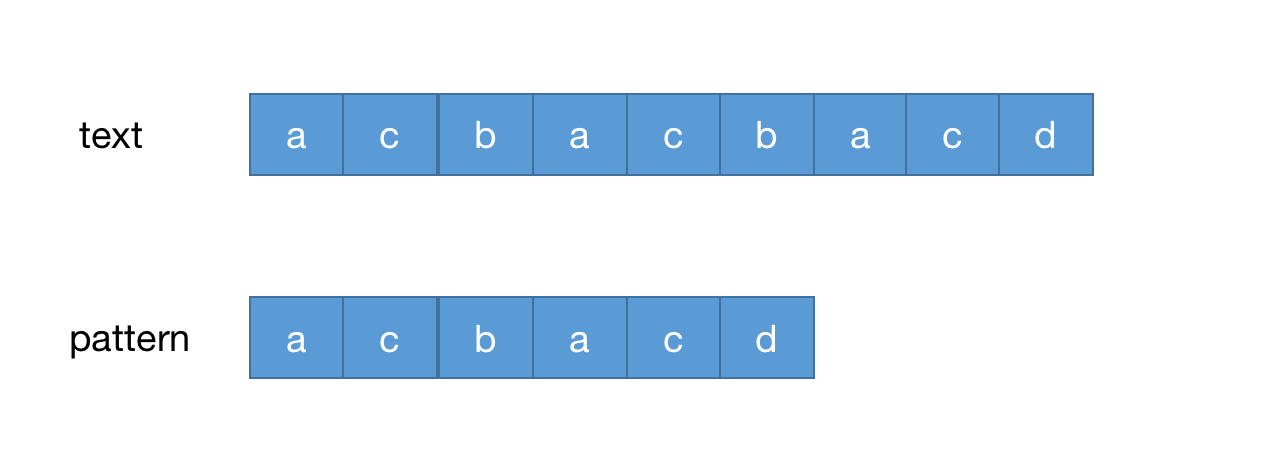
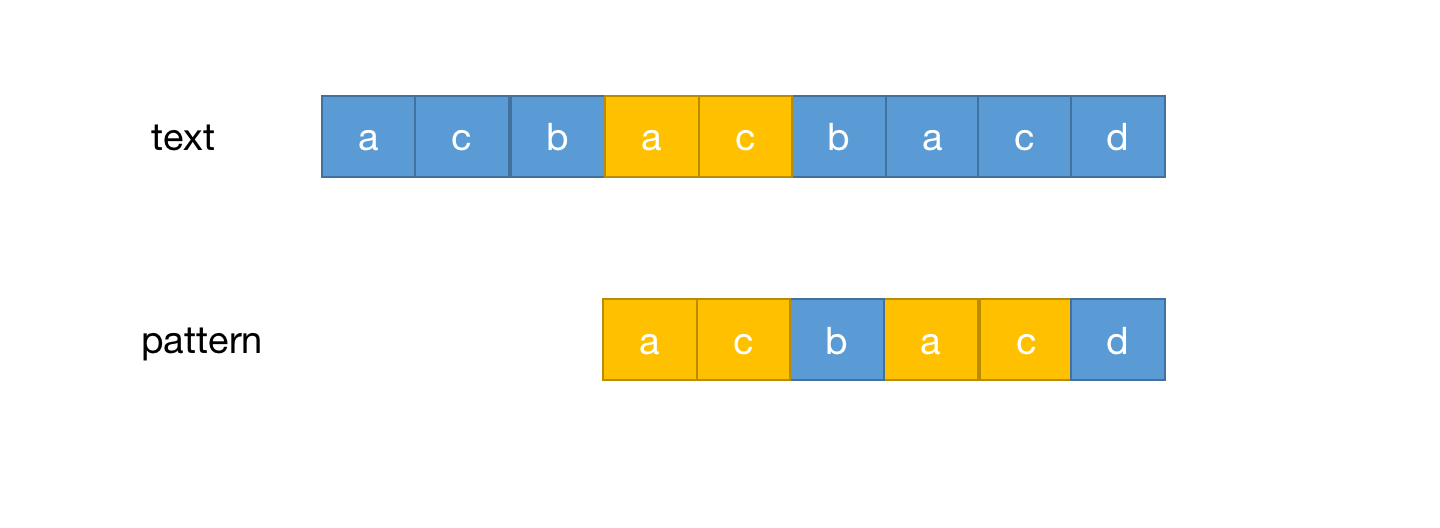
假设匹配的字符串为text，模式字符串为pattern，开始逐个匹配，当匹配到b和d时不匹配，如下图
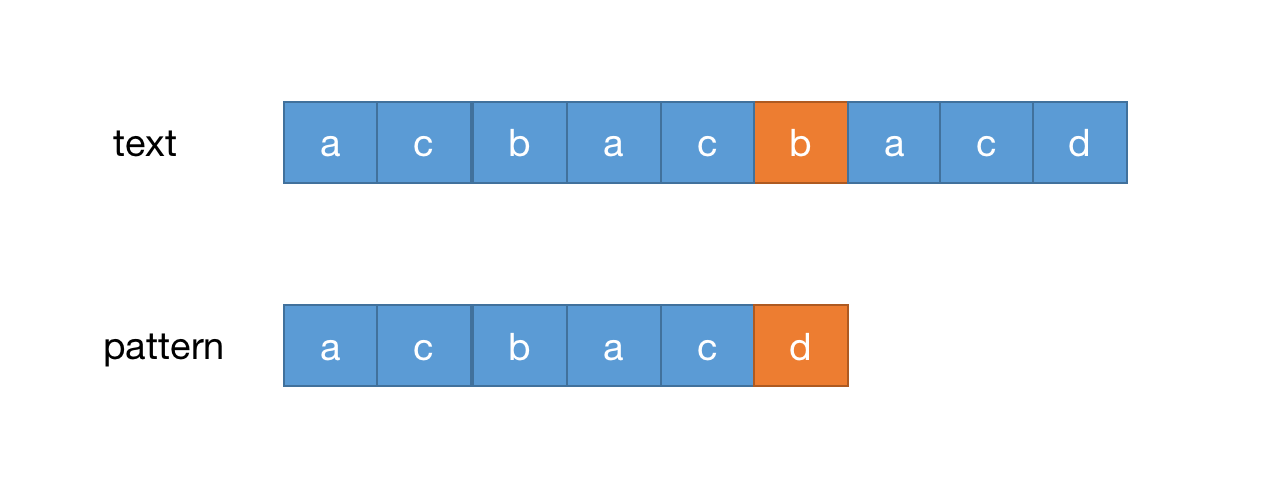
按暴力匹配的逻辑碰到不匹配的情况后把pattern后移一位继续匹配，如下图
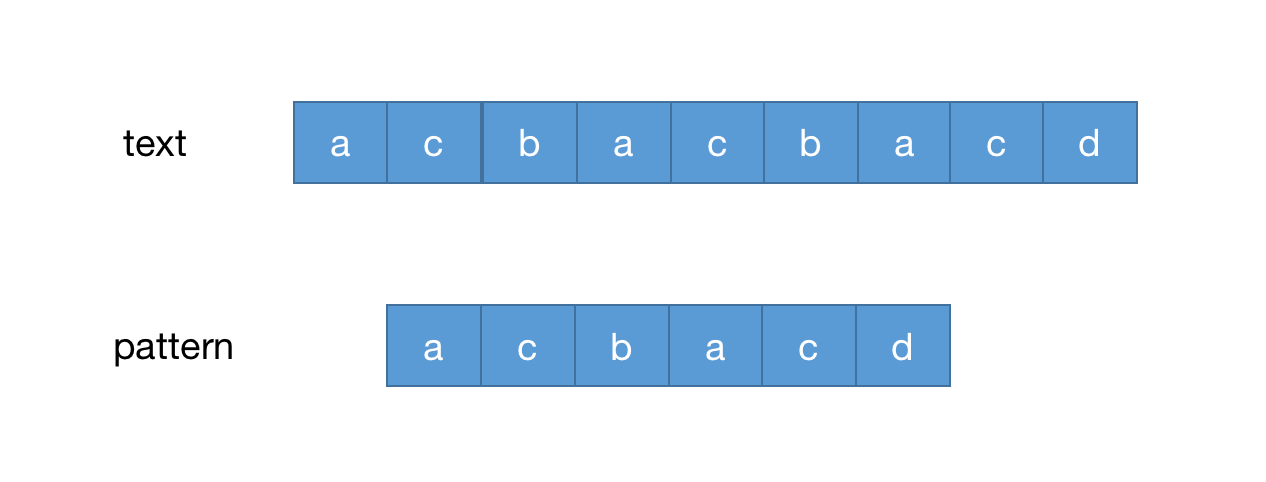
这样做虽然可以得到我们想要的答案，但是字符串匹配作为常用于操作系统的算法在面对字符串长度巨大的情况下的时间复杂度一定是巨大并影响系统性能的，那么就需要更好的算法来提高匹配速度，所以上面提到的算法就应运而生。

KMP

KMP算法(Knuth-Morris-Pratt算法)相比其它比如BM算法简单的多，因为它的核心思想很简单，只需要找出相同前缀，而相同前缀的意义在于如果匹配中出现不匹配的情况，可以根据已经匹配的序列中查找是否有相同的前缀，如果有直接把模式字符串pattern往后移动一段距离，距离的计算公式为:

移动距离 = 已经匹配序列的长度 - 相同前缀个数

再看回上面那个例子，在pattern中是存在相同前缀的，如下图
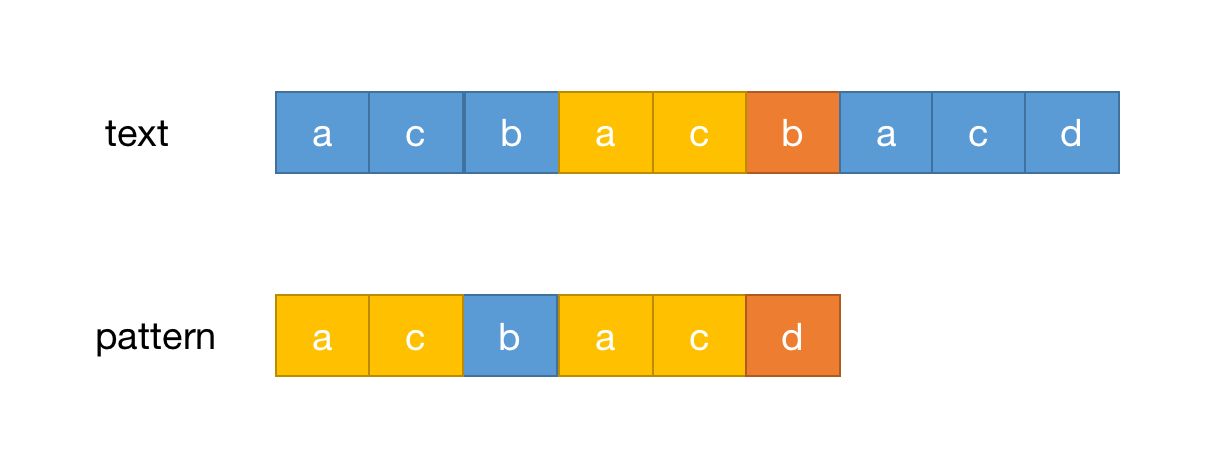
按照上面的公式，已经匹配的长度为5，相同前缀个数为2，计算出移动距离为3，移动后如下图
经过这么往后移动就直接匹配上了(当然这只是一个最简单的例子方便理解)，相比暴力求解的方式的效率确实高不少，那么现在重点来了，只要知道已匹配的序列中有多少个相同前缀就好办了。所以在开始把text和pattern匹配前需要对pattern内部进行一次相同前缀搜索，步骤如下：

建一个lps数组，即longest proper prefix，lps[i]表示的是pattern[0,i]中最长的和前缀相同的后缀，而因为第一个字符是不存在相同前缀的，所以lps[0]默认为-1
定义一个j，初始值为-1，这个j值代表的是相同前缀的最后一个索引，而一个字符串有可能不存在相同前缀，所以初始值定义为-1，然后从pattern第二个字符开始遍历，遍历的时候会有两种情况：
- 第一种是pattern[i]===pattern[j+1],如下图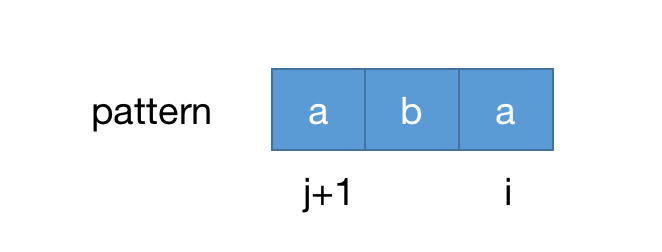
  当匹配相等的时候j++，然后lps[i]=j
- 第二种是pattern[i]!==pattern[j+1]&&j>-1 首先解释下为什么会有一个j>-1的条件，因为j>-1代表的是在这个匹配项前已经存在一个相同前缀值，如果j===-1&&pattern[i]!==pattern[j+1],也就是不存在相同前缀且当前匹配项不相等，那么直接走到最后一步lps[i]=j即可。
  
  回到上面的条件如果pattern[i]!==pattern[j+1]&&j>-1，那么j=lps[j]，这段逻辑怎么去理解呢，如下图：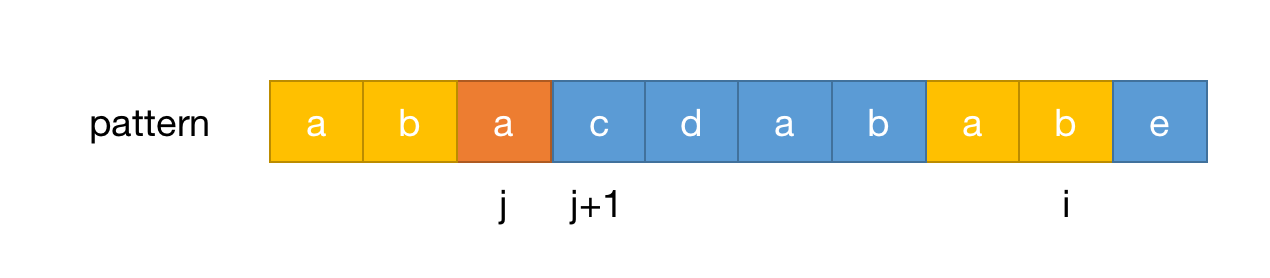
  可以看到当匹配到c和b是不相等的，但是如果往前一看[i-1,i]这个区间是存在相同前缀的，j=lps[j]就是把j回退到前一个相同前缀索引继续循环 pattern[i]是否等于pattern[j+1]，简单来说就是看看前面已经得出的相同前缀有没有可以复用的。
  
  上图的j索引为2，这个时候pattern[j+1]!==pattern[i]，而j等于2的时候已经匹配的前缀为aba，这个前缀的相同前缀为a，那么就要把j回退，回退后为j=0,然后继续判断pattern[j+1]是否等于pattern[i]，那么这个时候是相等的，所以可以算出前缀为abacdabab的时候复用了一个为ab的相同前缀。
最后lps[i]=j,当循环结束后lps数组就计算完成，如下图：

把lps数组计算出来后text和pattern的匹配思路简单了，同样对text遍历一次，如果判断出text[i]!==pattern[j+1]时就通过lps找出有没有相同前缀，如果有则pattern往后移动继续比较，当j===pattern.length-1的时候代表j就是pattern在text中第一次出现的位置。

代码实现

let cal_lps = function (str, len, lps) {
    let j = -1;
    lps[0] = -1;
    for (let i = 1; i < len; i++) {
        while (j > -1 && str[j + 1] !== str[i]) {
            j = lps[j]
        }
        if (str[j + 1] === str[i]) {
            j++
        }
        lps[i] = j
    }
};

let strStr = function (haystack, needle) {
    if (!needle.length) {
        return 0
    }
    let hlen = haystack.length,
        nlen = needle.length,
        j = -1,
        lps = new Array(nlen);
    cal_lps(needle, nlen, lps);
    for (let i = 0; i < hlen; i++) {
        while (j > -1 && haystack[i] !== needle[j + 1]) {
            j = lps[j];
        }
        if (haystack[i] === needle[j + 1]) {
            j++
        }
        if (j === nlen - 1) {
            return i - j
        }
    }
    return -1
};

# 题目：实现 strStr()

# 解题思路

# KMP

# 代码实现

题目：实现 strStr()

解题思路

KMP

代码实现