22.括号生成 | LeetCode题解

题目：括号生成

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/generate-parentheses/

解题思路

注：这条题出于画图方便理解的原则将使用动态规划求解，后面会大致说一下深度遍历的思路并附上代码，至于理解与否就要靠各位看官自己脑洞了，因为画图真的太抽象了～～

动态规划

OK，那么动态规划怎么用在这条题目上呢，动态规划的思想是在无后效性进行状态转移，就拿这条题目来说，可以理解为这样：

在求n组括号的排列组合前已知n-1组排列组合已经完成求解，所以这个时候求n的排列组合的解要考虑的其实就是n-1的排列组合应该放在第n个括号的什么位置

n-1的排列组合可以分为两部分：B个括号的排列组合和C个括号的排列组合:

"("+B个括号的排列组合+")"+C个括号的排列组合

B+C=n-1，并且B和C分别第n个括号的里面和右边，步骤如下：

n=2，把第2个括号拿出来
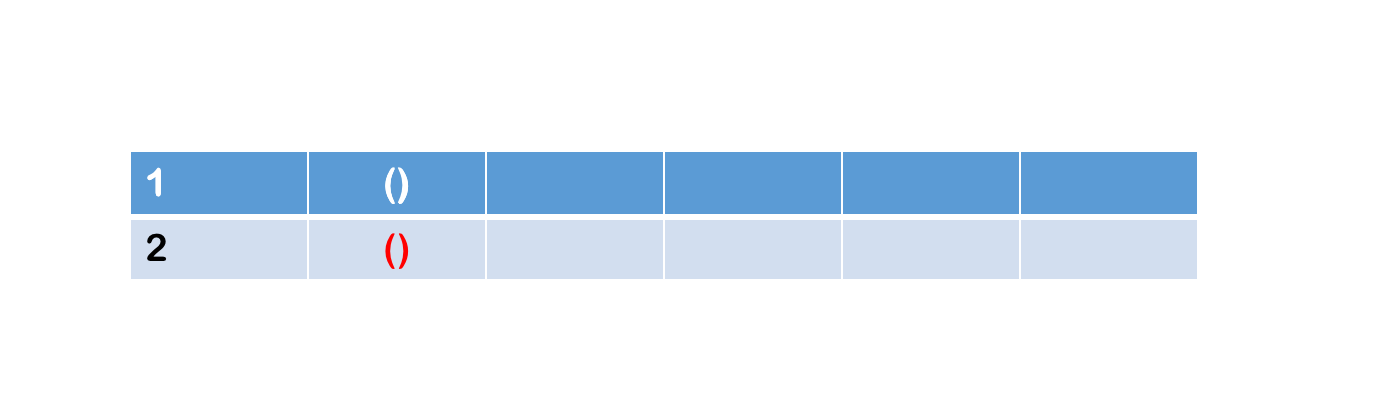
已知B+C=n-1，情况只有两种，B=1，C=0或B=0,C=1，那么组合完如下图：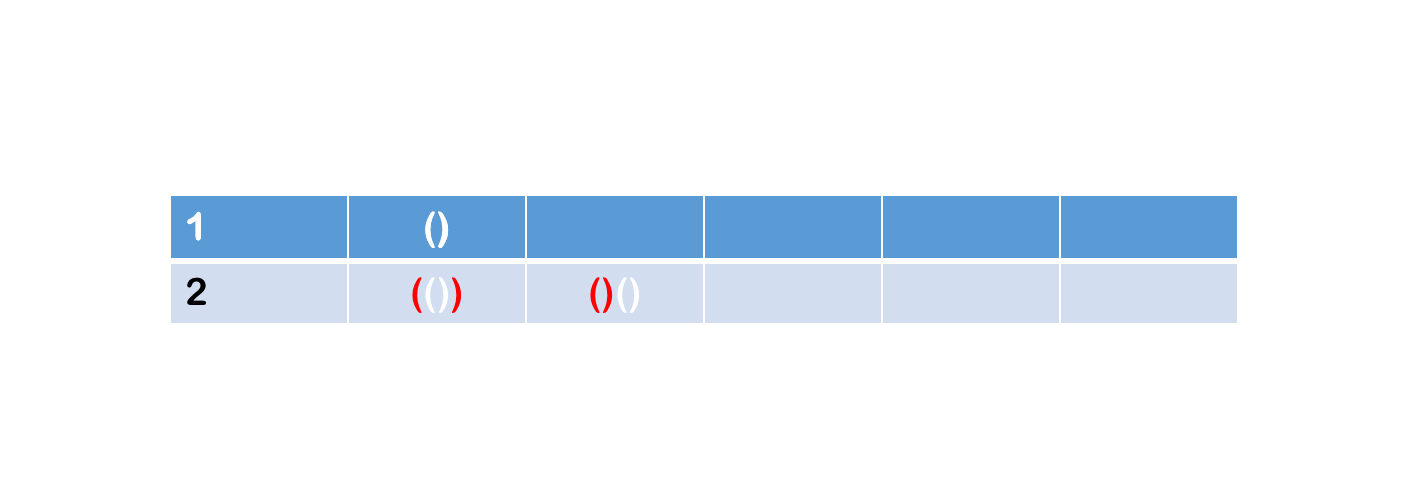
当n=3时，B+C=n-1的情况就开始多了，下面逐个列举，当B=0,C=2时组合如下：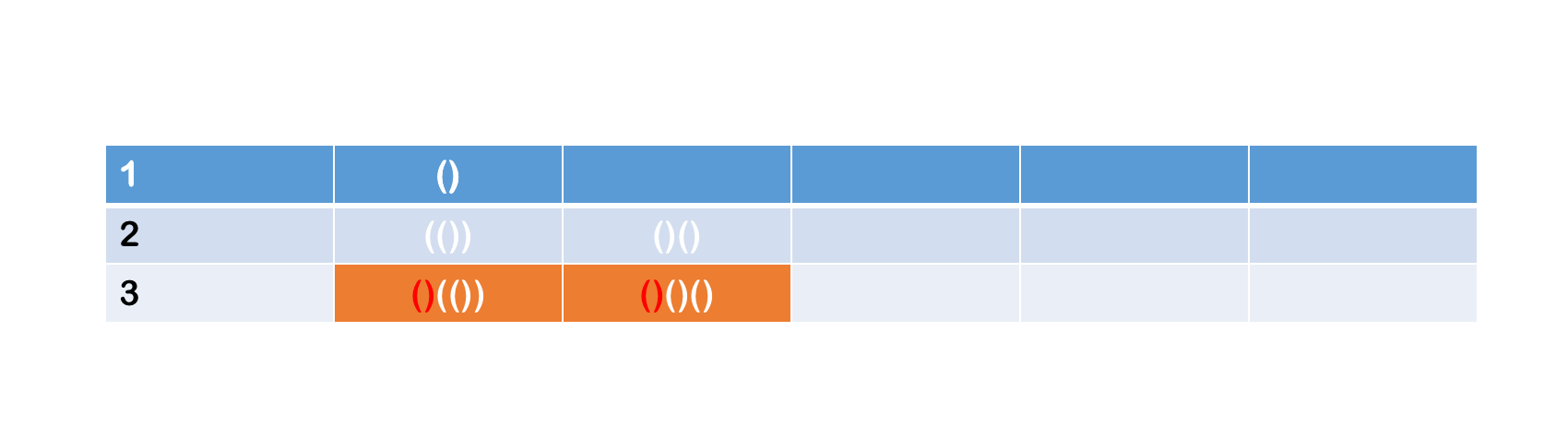
当B=1,C=1时：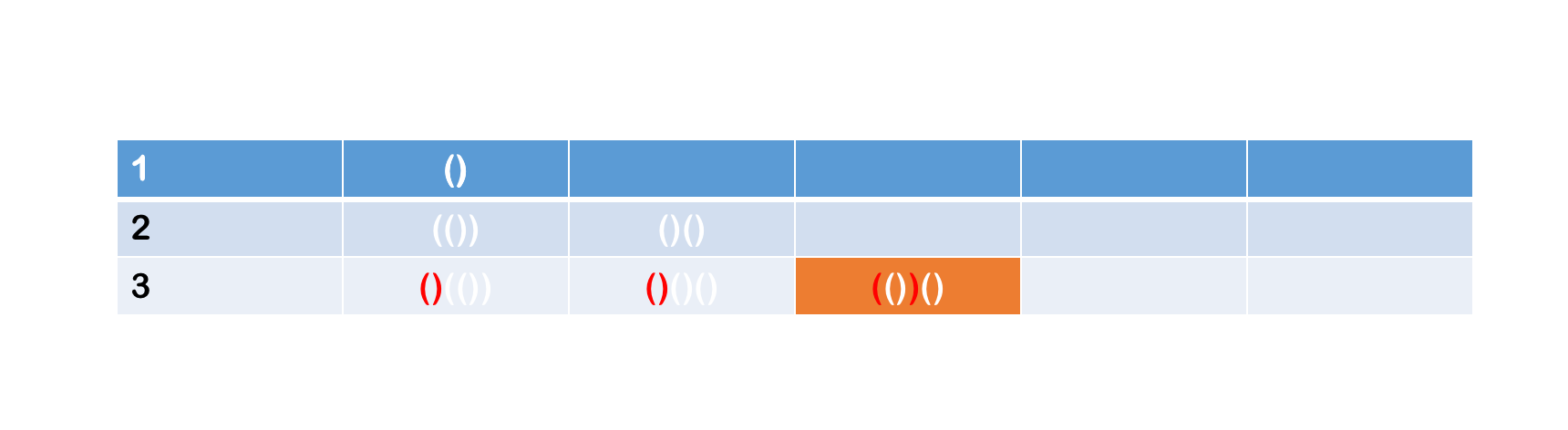
当B=2,C=0时：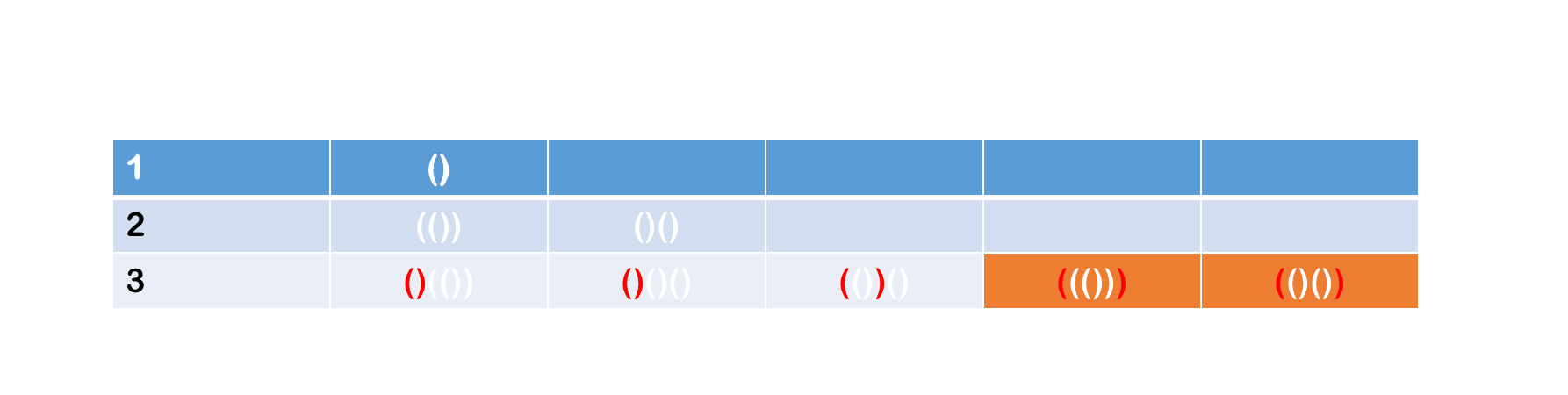
那么根据上面列举的步骤，B从0列举到n-1，C从n-1列举到0，然后它们的结果组合在一起

使用动态规划求解的巧妙在于想的不是把第n个括号放在n-1个括号的哪里，而是n-1个括号分别放在第n个括号的里面和外面，这样就可以把n-1个括号进行拆分组合出不同的数值加法(比如3=1+2，也可以是3+0)，同时利用之前的计算结果得出当前结果，最后算出最终结果

深度遍历

深度遍历的思想核心是先去先定义l和r代表左括号和右括号还可以进行拼接的数量，先用左括号进行拼接，当递归终止后再进行右括号拼接，而递归终止的条件一般只有两个，l=0&&r=0或l>r，l=0&&r=0容易理解，l>r则代表右括号可组合的数量已经少于左括号，那么这个时候应该要终止递归回到上一层继续先进行左括号的拼接

代码实现1：动态规划

const generateParenthesis = (n) => {
    let dp = [];
    dp[0] = [''];
    dp[1] = ['()'];
    for (let i = 2; i <= n; i++) {
        dp[i] = [];
        for (let j = 0; j < i; j++) {
            for(let p of dp[j]){  // B=J
                for(let q of dp[i-1-j]){  // B+C=n-1 ==> C=i-1-B
                    dp[i].push(`(${p})${q}`)
                }
            }
        }
    }

    return dp[n]
};

代码实现2：深度遍历

const generateParenthesis = (n) => {
    let res = [];
    generate('', n, n, res);
    return res;
};

const generate = (str, l, r, res) => {
    if(l > r) return;
    if (!l && !r) res.push(str);
    if (l) generate(str + '(', l - 1, r, res);
    if (r) generate(str + ')', l, r - 1, res);
};

# 题目：括号生成

# 解题思路

# 动态规划

# 深度遍历