# 题目：盛最多水的容器

给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。 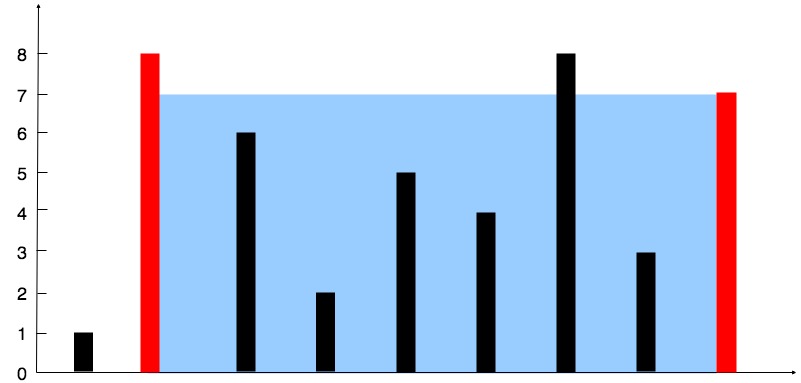图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例1：

输入: [1,8,6,2,5,4,8,3,7]
输出: 49

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/container-with-most-water/

# 解题思路：双指针法

首先假设高为h，两线距离为len，我们知道求体积v的公式是h*len，那么根据公式可以知道如果要求出最大体积那么len应该是尽可能的长，但是由于受到h的限制只能取相对短一端来计算
先初始设置左右两线位置为l=0和r=height.length-1如下图: 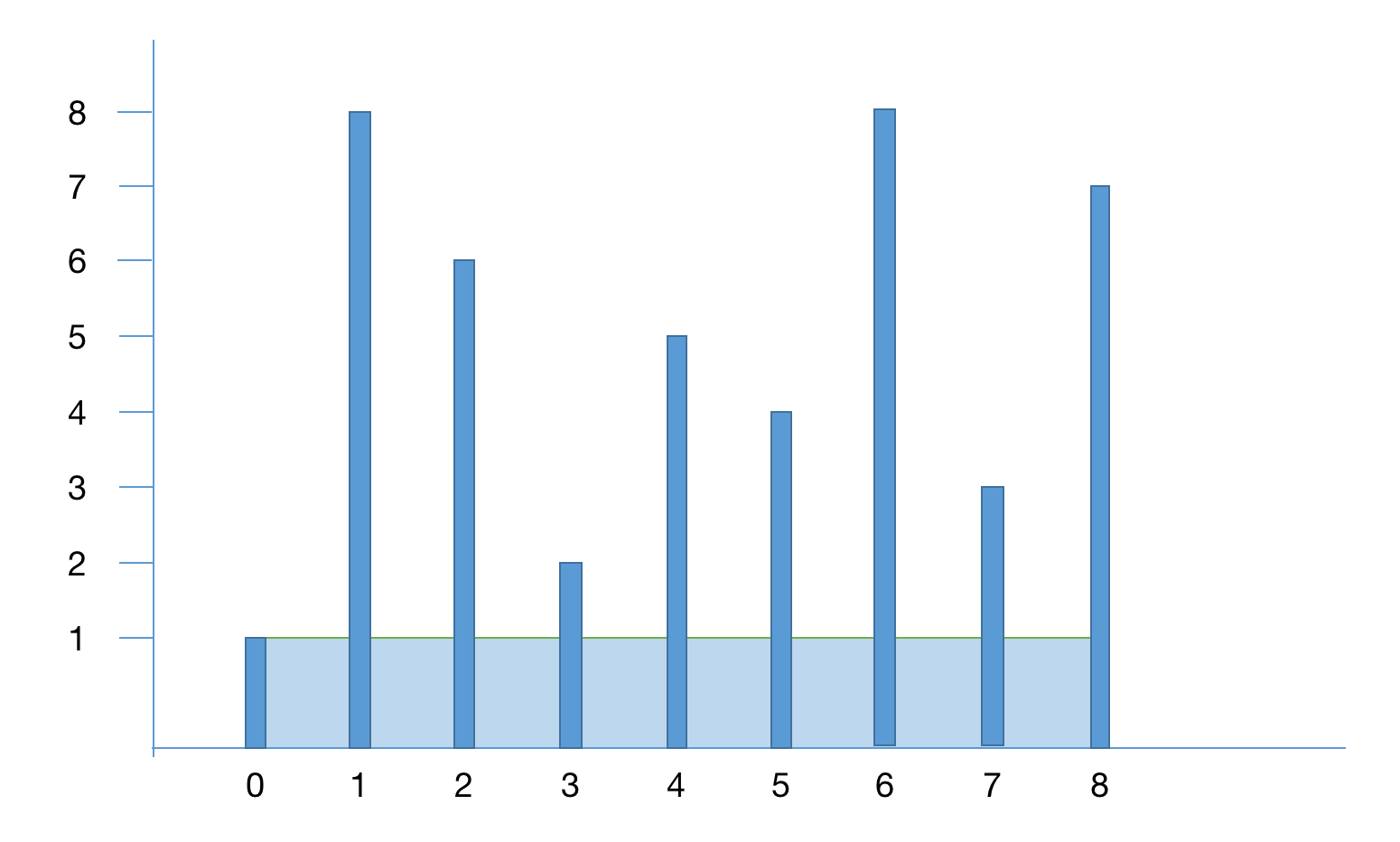如上图，先从h[l]和h[r]取最短的作为h，那么v=h[l]*(r-l)=8,在计算完后l往右移动，为什么是l往右移动而不是r往左移动呢呢，因为已知计算v时h应取最短一侧，那么当前长度已为最远情况下h不变就不可能超过原来的值 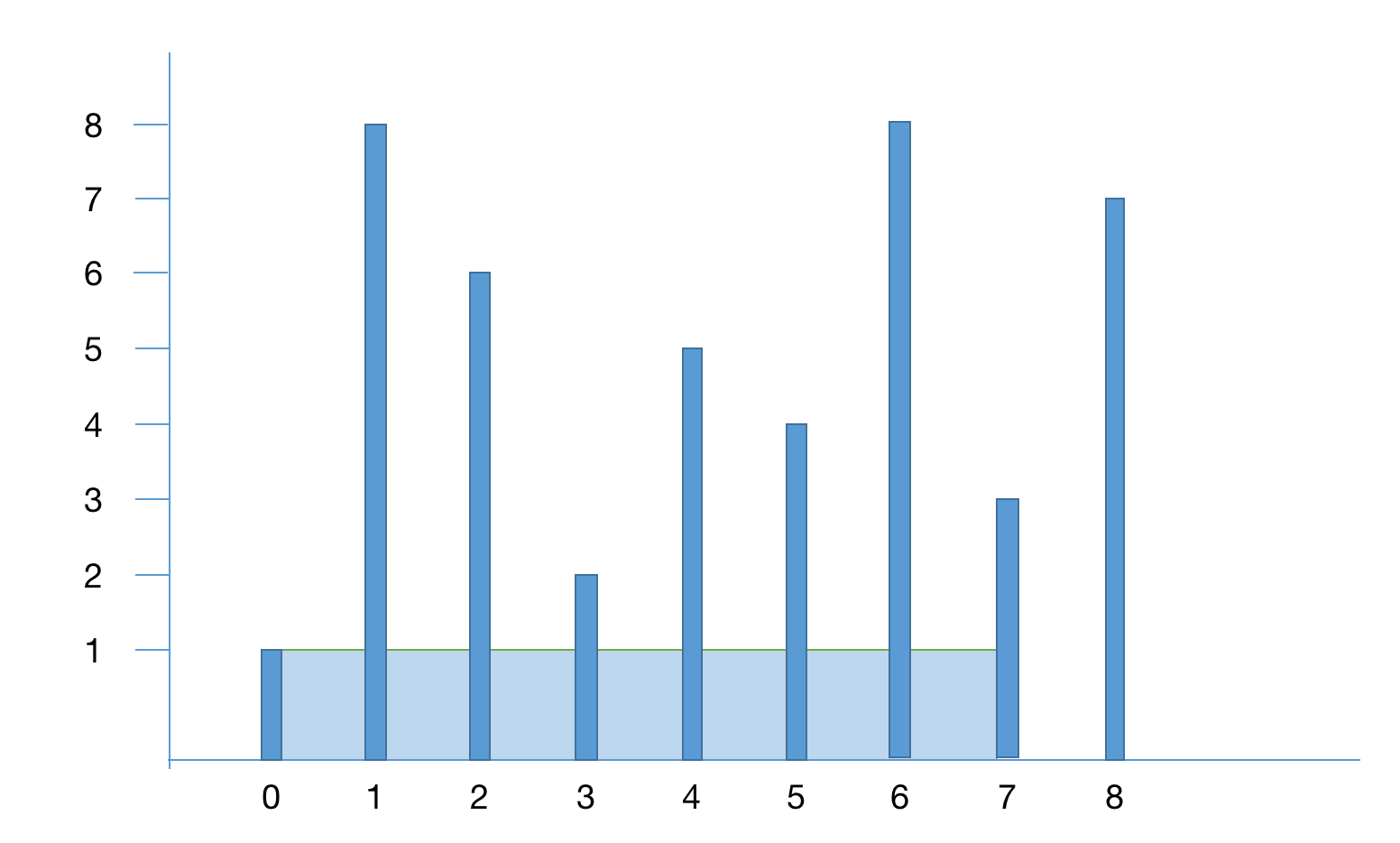如上图，假设r往左移动，那么按上面的公式计算出的结果v=7,所以要取得最大体积只能把短的一边舍弃寻找更高的值 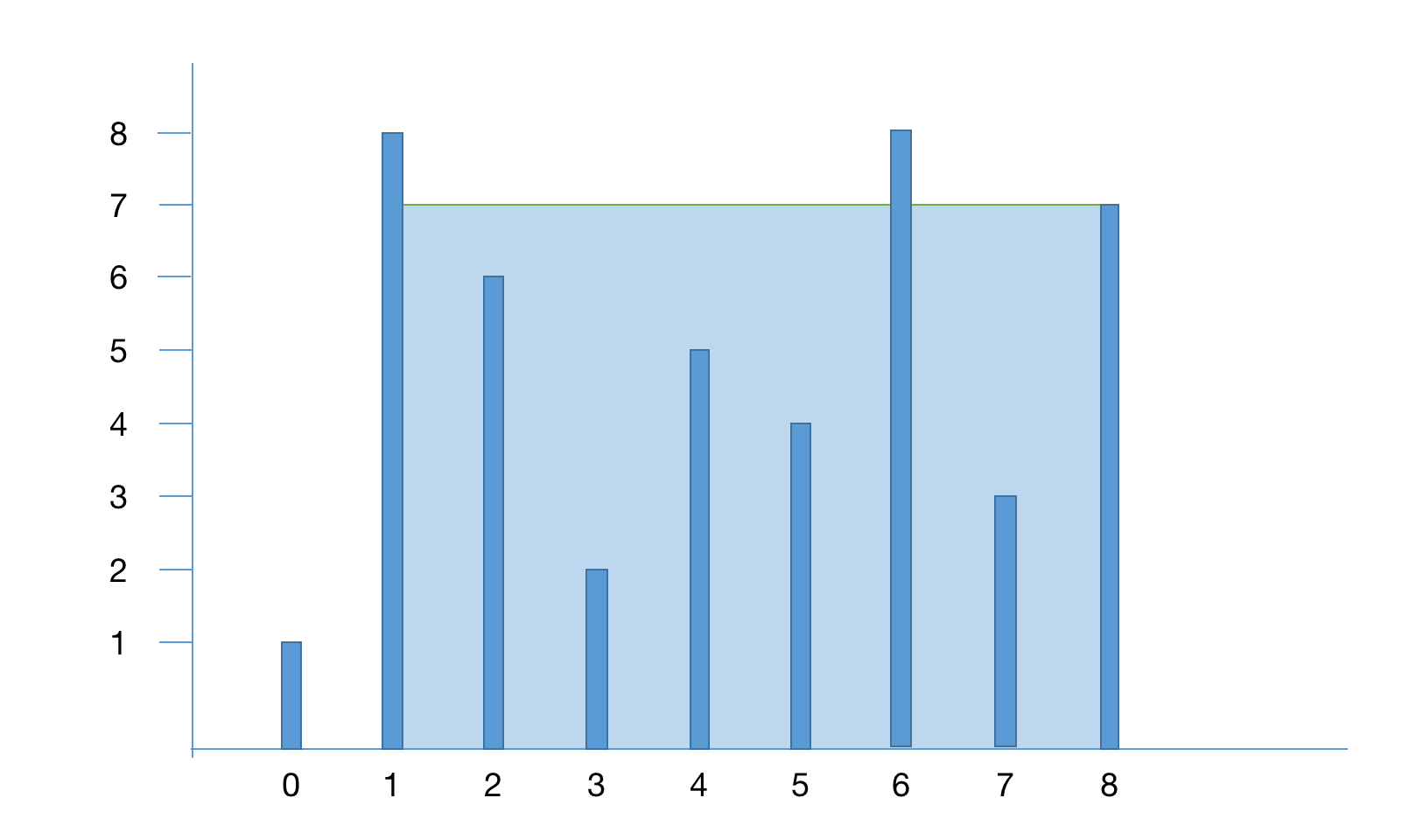如上图l往左移动后v=h[r]*(r-l)=49，那么这个值是大于之前计算的v

# 代码实现

let maxArea = function (height) {
    let h1 = 0,
        h2 = 0,
        w = 0,
        v = 0,
        maxv = 0,
        l = 0,
        r = height.length - 1;
    while (r - l > 0) {
        h1 = height[l];
        h2 = height[r];
        if (h1 > h2) {
            v = h2 * (r - l)
            r--
        } else {
            v = h1 * (r - l)
            l++
        }
        maxv = Math.max(maxv, v)
    }
    return maxv
};