10.正则表达式匹配 | LeetCode题解

题目：正则表达式匹配

给你一个字符串s和一个字符串类型匹配模式p，请你来实现一个支持'.'和'*'的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖整个字符串s的，而不是部分字符串说明:

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。

示例1：

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

示例 2：

输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3：

输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）

示例 4：

输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

示例 5：

输入:
s = "mississippi"
p = "mis*is*p*."
输出: false

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/regular-expression-matching/

解题思路:动态规划

首先解题要先理解正则表达式具体匹配规则,先来做个最简单的假设:

假设s=ab,p=a*b*,那么毫无疑问s.match(p)是成立的
根据上面的例子,p变成a*b*c,那么这就是不成立的，因为s并没有c，如果p再加一个*变成a*b*c*，那么匹配又会变成立，因为c这个时候可以匹配为0个
那么当匹配到*号的时候具体到代码上逻辑是这样的:

if(p.charAt(i) === '*'){
  dp[i+1] = dp[i-1]
}

以上的逻辑思路就是当匹配到a*b*c*中时，判断最后一个*是否匹配成立只需要看第2个*,即a*b*是否匹配，如果匹配那么a*b*c*也是成立的,假如s换成是ad，那么走到a*b的时候就已经不匹配了,经过状态转移a*b*c*也不会匹配，所以使用 动态规划 就再合适不过

第一步：建立二维数组

假设s=abbcddd,p=a*b*.dd*,因此先建立一张对应二维数组的表:
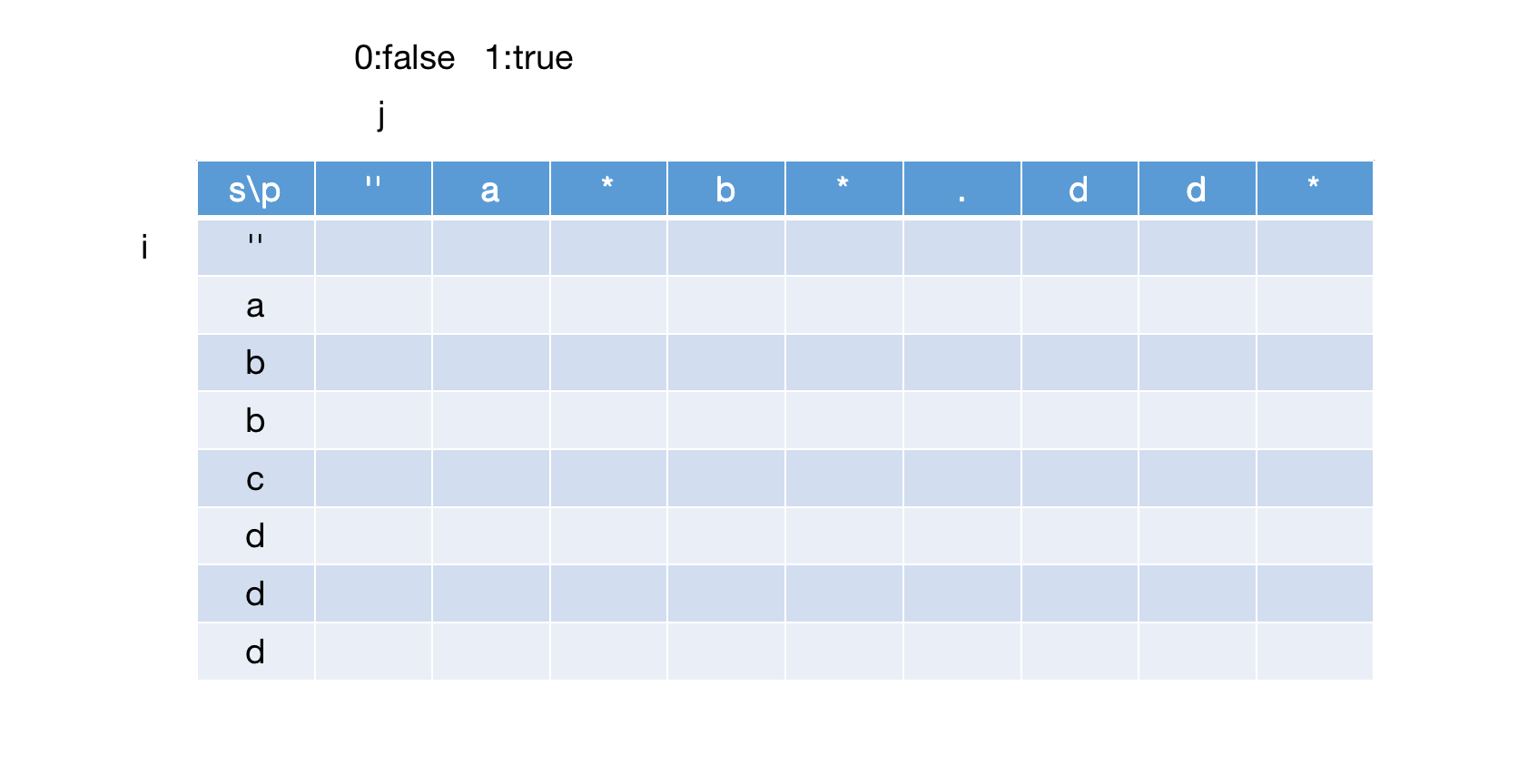为何要在p前面加一个空字符串(只是在表格中加)，原因也很简单，假设当s='',p=a*时匹配是成立的，那么根据上面的逻辑dp[0][j+1]=dp[0][j-1],那么就需要一个空值为true才能确保转移到a*后仍然为true
然后先建立一种简单的匹配情况，字符可以先把s假设为空字符串，p不变，那么可以s匹配p的结果如下(假设0为false,1为true):
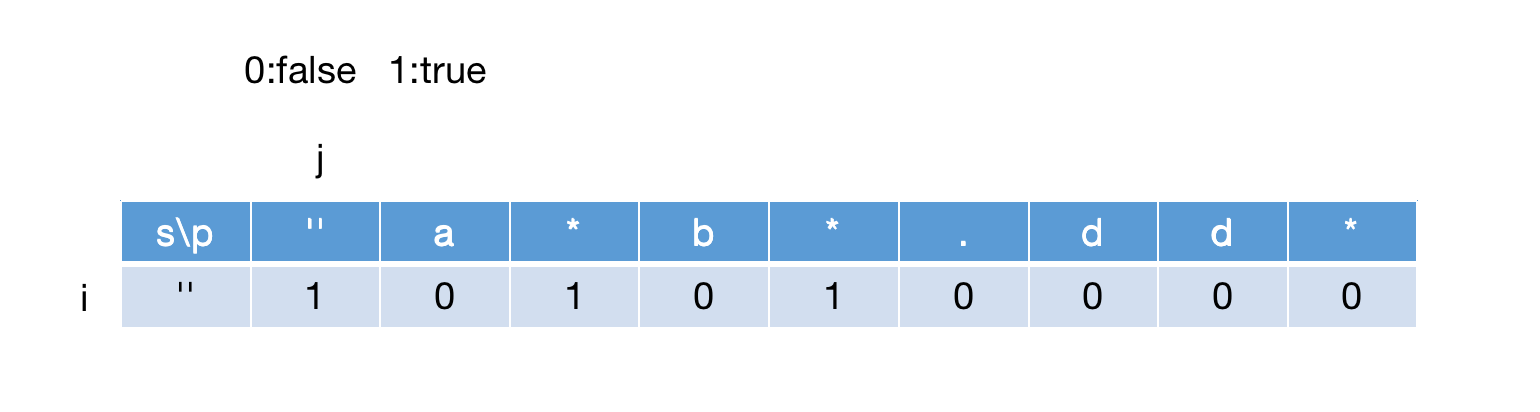如上图，当p[j]='.'的时候可以当成是任意字符串但不能为空，因此匹配也为false，结合上述逻辑，一开始先匹配第一个空字符的逻辑可以总结为:

    dp[0][0] = true;
    for (let i = 1; i < p.length; i++) {
        if (p.charAt(i) === "*") {
            dp[0][i + 1] = dp[0][i - 1]
        }
    }

这个时候匹配完的dp[0]意义就是后续dp[i][j]进行状态转移的判断依据

第二步: 匹配状态转移

在dp[0]全部赋值后开始对字符串s和模式字符串p进行逐一匹配，那么匹配过程一共会碰到三种情况:

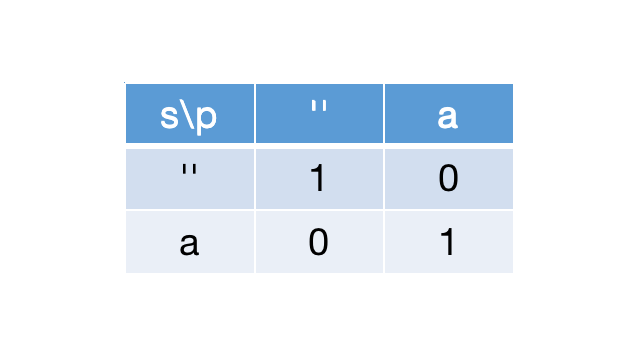
p[j]为普通字符时:
如果s[i]===p[j],那么通过dp[i+1][j+1]=dp[i][j]判断，例子如下图：
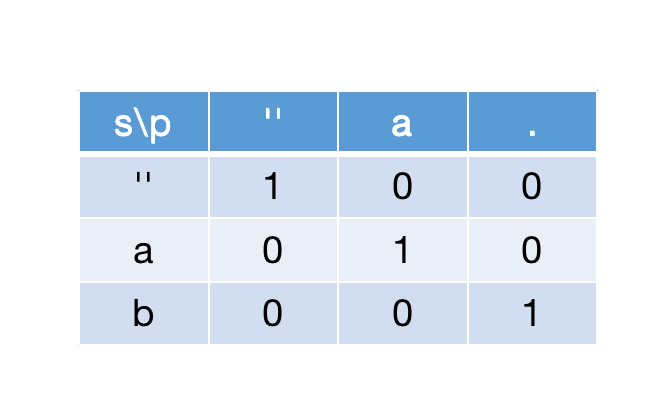
p[j]为.时:
可以把p[j]看成任意但不为空的字符，也是通过dp[i+1][j+1]=dp[i][j]判断，例子如下图：
p[j]为*时:
1.如果p[j-1]!==s[i]&&p[j-1]!=='.'时，和上面的dp[0][j+1]=dp[0][j-1]的逻辑一样，把前一个*的状态值转移过来，如下图:
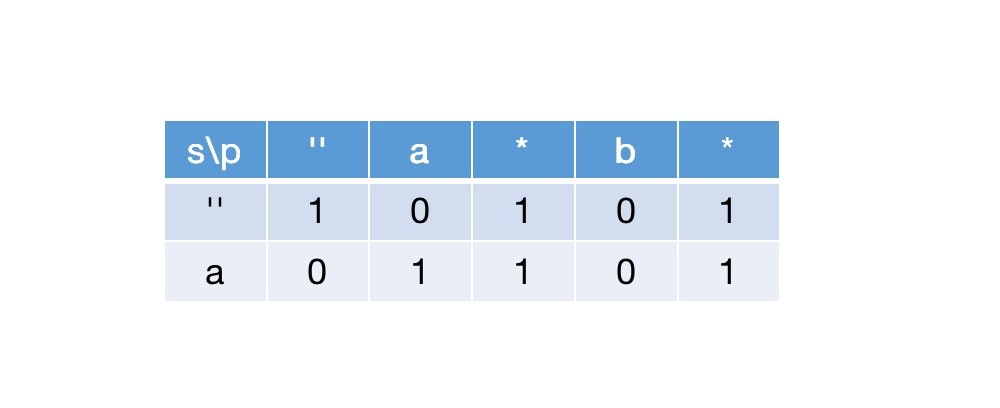当i=0,j=3时,s[0]!==p[2]，因此dp[i+1][j+1]=dp[i+1][j-1]=1

2.当p[j-1]==s[i]时，对*可以匹配成功的情况可以分为三种，假设p[j-1]=b，出现的个数为n:
- n=0时，复用上面的逻辑，即dp[i+1][j+1]=dp[i+1][j-1]
- n=1时，dp[i+1][j+1]只需要等于dp[i+1][j]的值即可，如下图：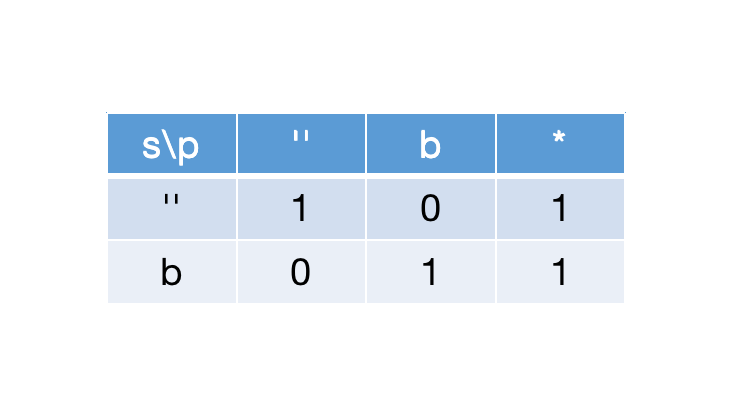
- n>=2时，这个时候dp[i+1][j]和dp[i+1][j-1]都有可能为false，如下图: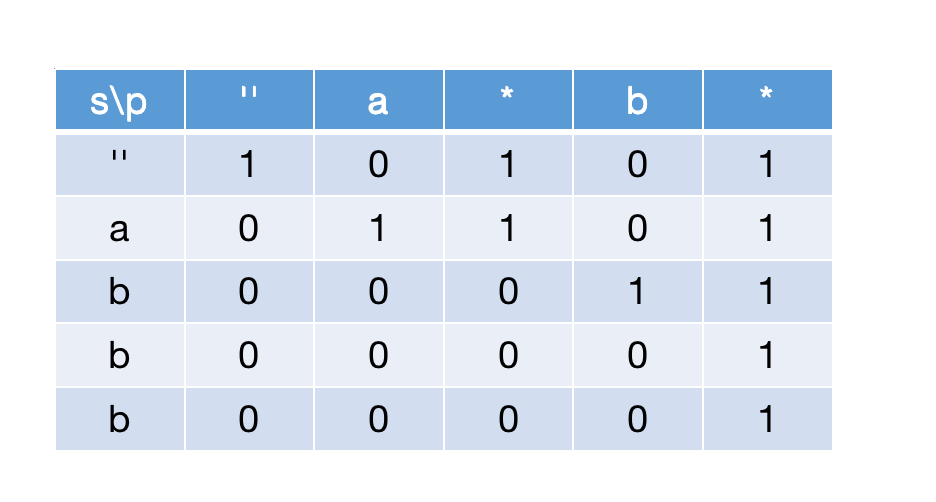 那么在出现多个b后dp[i+1][j+1]可以根据dp[i][j+1]判断
  综上所述，当p.charAt(j) === '*'时，具体逻辑可以归纳为:
```
  if (p.charAt(j - 1) !== s.charAt(i) && p.charAt(j - 1) !== '.') {
      dp[i + 1][j + 1] = dp[i + 1][j - 1]
  } else {
      dp[i + 1][j + 1] = (dp[i + 1][j] || dp[i][j + 1] || dp[i + 1][j - 1])
  }
```

匹配完成后返回dp[s.length][p.length]就是最终结果。

代码实现

let isMatch = function (s, p) {
    let dp = Array(s.length + 1);
    for (let i = 0; i < dp.length; i++) {
        dp[i] = Array(p.length + 1).fill(false)
    }
    dp[0][0] = true;
    for (let i = 1; i < p.length; i++) {
        if (p.charAt(i) === "*") {
            dp[0][i + 1] = dp[0][i - 1]
        }
    }

    for (let i = 0; i < s.length; i++) {
        for (let j = 0; j < p.length; j++) {
            if (p.charAt(j) === '.') {
                dp[i + 1][j + 1] = dp[i][j]
            }

            if (p.charAt(j) === s.charAt(i)) {
                dp[i + 1][j + 1] = dp[i][j]
            }

            if (p.charAt(j) === '*') {
                if (p.charAt(j - 1) !== s.charAt(i) && p.charAt(j - 1) !== '.') {
                    dp[i + 1][j + 1] = dp[i + 1][j - 1]
                } else {
                    dp[i + 1][j + 1] = (dp[i + 1][j] || dp[i][j + 1] || dp[i + 1][j - 1])
                }
            }
        }
    }
    return dp[s.length][p.length]
};

# 题目：正则表达式匹配

# 解题思路:动态规划

# 第一步：建立二维数组

# 第二步: 匹配状态转移

# 代码实现

题目：正则表达式匹配

解题思路:动态规划

第一步：建立二维数组

第二步: 匹配状态转移

代码实现