题目:最长回文子串
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-palindromic-substring/
解题思路1:中心扩展法
首先要了解什么是回文串,通俗的话讲就是对称字符串,比如aba为回文串,abba也是回文串,因为它们在反转后仍然相等,即
str === str.reverse()
满足上诉条件就是回文串,而回文串又分为两种情况
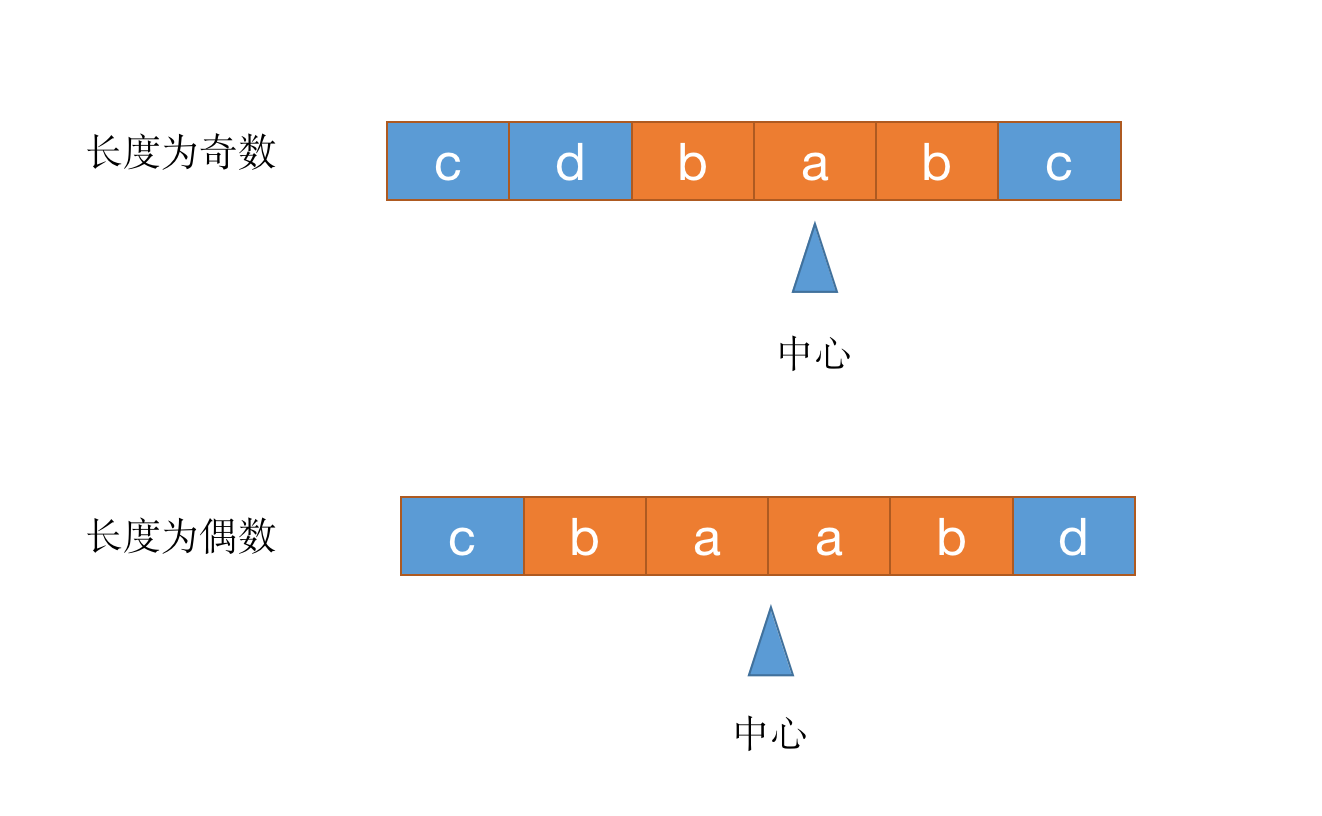
如上图,当长度为奇数的时候中心为a,为偶数的时候中心是a和a的边界,因此在计算的时候就需要同时考虑两种情况
首先定义start和maxLen,start用于记录最长回文串起点,maxLen用于记录最大长度
每次循环去执行一个函数,函数同时执行两次,传入中心点为i和i,i和i+1
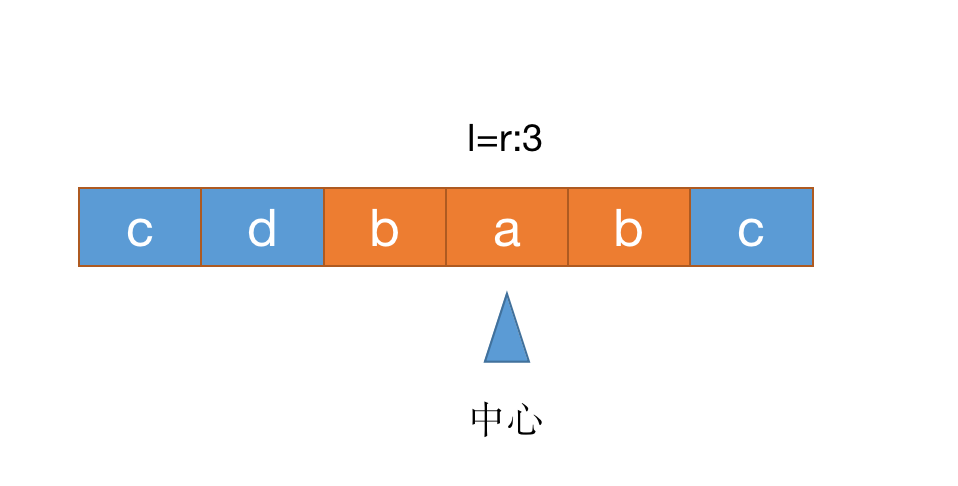
如上图,以长度为奇数为例子,传入的i和i分别当作l和r,当s[l]===s[r]时,l移动至前一位,r移动至后一位,如下图
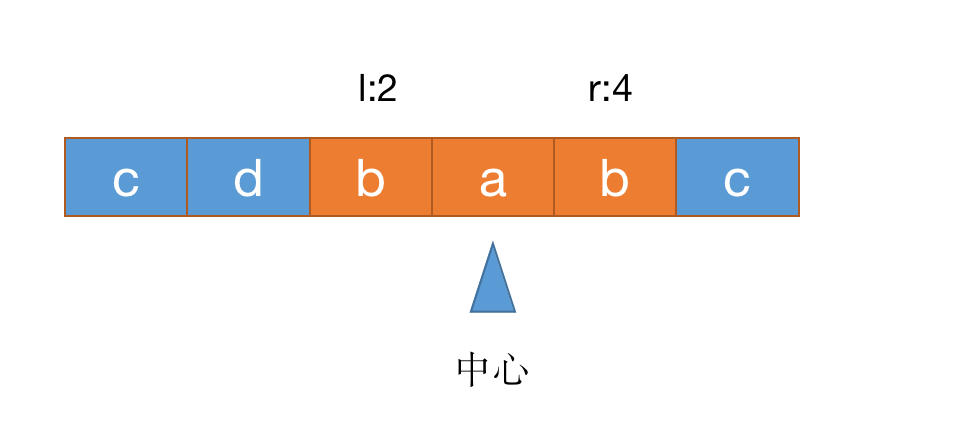
继续比较s[l]和s[r],相等则继续移动,如下图
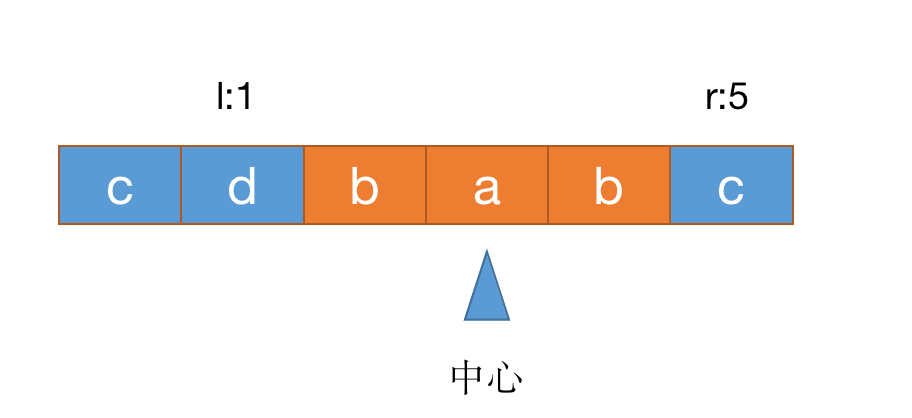
继续比较,s[l]!==s[r],退出循环
然后与maxLen与r-l-1比较,如果后者更大则更新maxLen,同时更新start为l+1
解题思路2:Manacher算法
Manacher算法简介
[Manacher(1975)] 发现了一种线性时间算法,可以在列出给定字符串中从字符串头部开始的所有回文。并且,Apostolico, Breslauer & Galil (1995) 发现,同样的算法也可以在任意位置查找全部最大回文子串,并且时间复杂度是线性的。因此,他们提供了一种时间复杂度为线性的最长回文子串解法。替代性的线性时间解决 Jeuring (1994), Gusfield (1997)提供的,基于后缀树(suffix trees)。也存在已知的高效并行算法。
Manacher(又称"马拉车")算法对比中心扩展法来看更可以认为是一种结合kmp的优化版,对比中心扩展法时间复杂度是O(n^2),马拉车算法时间复杂度为O(n)
第1步:添加分隔符
中心扩展法需要同时计算奇数长度和偶数长度的中心,马拉车算法开始计算前在字符串中插入分隔符#,就可以把奇数长度和偶数长度的字符串全部整合为一种情况,如下:
比如:
- 奇数长度:
bbbabbc=====>#b#b#b#a#b#b#c# - 偶数长度:
cbbabb=====>#c#b#b#a#b#b#
为什么需要加分隔符呢,简单做个计算:假如字符串长度是len,在每个字符前添加一个分隔符长度就会变为2*len,在字符串最后再加一个分隔符,长度就变为2*len+1,这样就确保字符串长度始终为奇数,可以不考虑之前偶数长度情况,往后计算会更加方便
第2步:建立p数组,得到任意字符串回文半径长度
建立p数组的意义在于得到任意字符串回文半径长度,因为每一个字符串本身都个可以看作是一个回文字符,而较前位置的回文字符半径会被较后位置的回文字符复用(由于回文字符性质,前半部分存在的回文字符在后半部分同样存在),因此复用半径可以直接减少while循环次数,直接降低时间复杂度
以cbbabb为例,先画出下面的表格
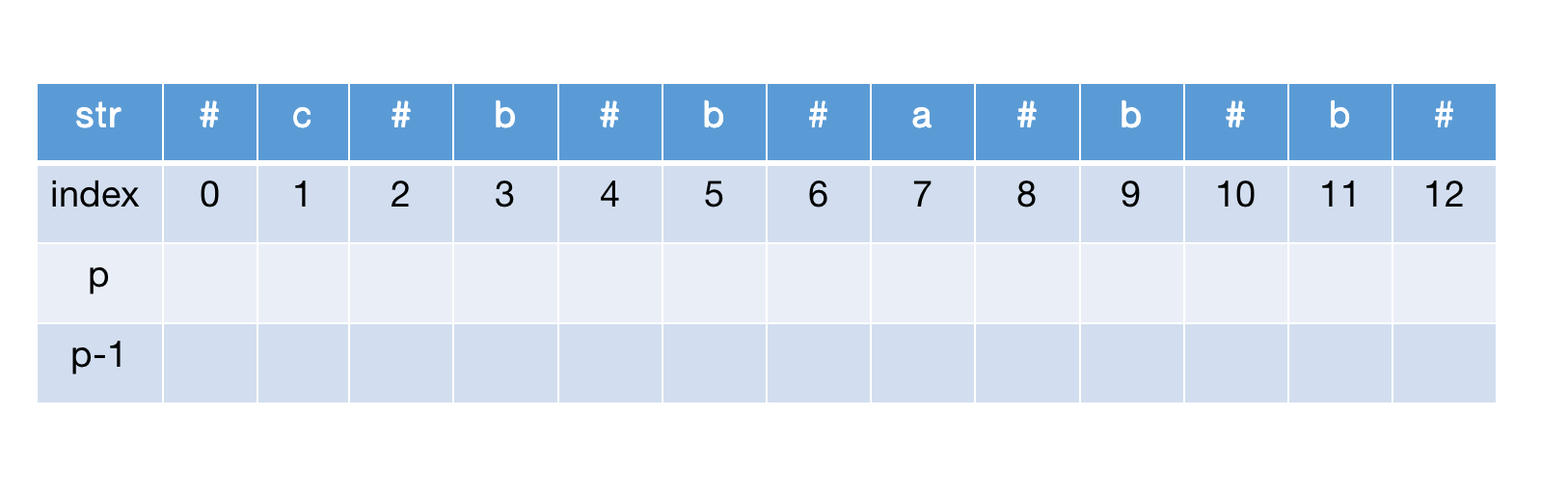
首先定义如何计算回文半径:
- 从字符串开始计算,以当前扩展点为中心,最小半径为1,然后同时往左右进行中心扩展,直至不能扩展为止
首先计算str[0],初始半径为1,然后进行中心扩展,结果都到了边界,因此str[0]半径为1
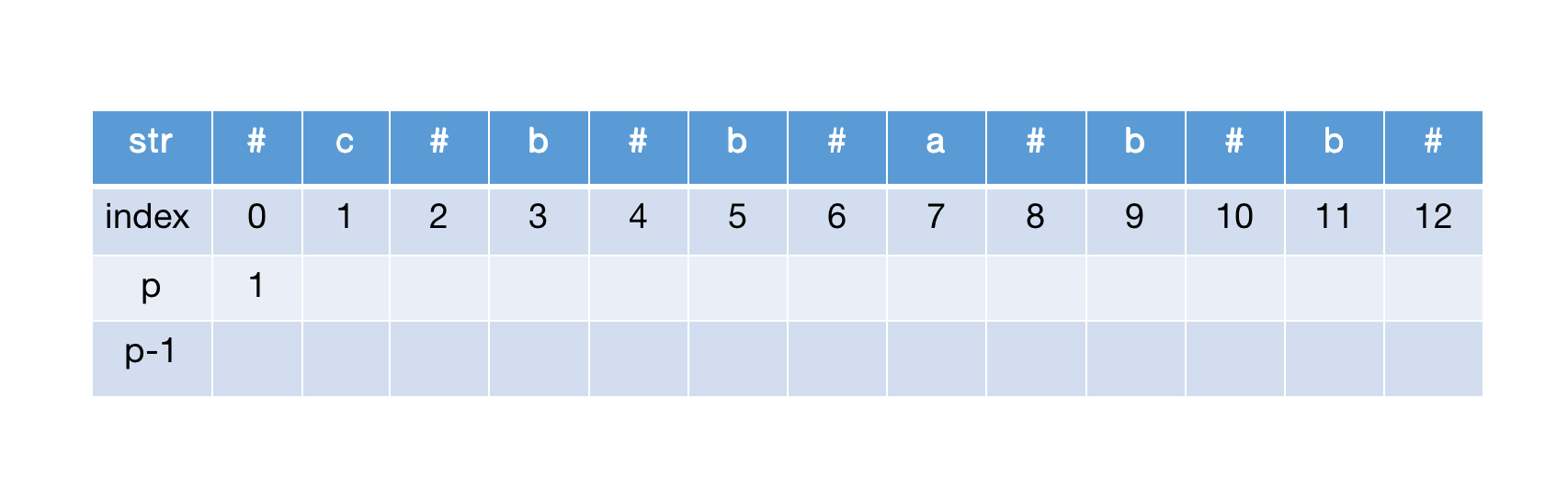
计算str[1],同样初始化半径后中心扩展,str[0]=str[2],半径加1,继续扩展到达边界
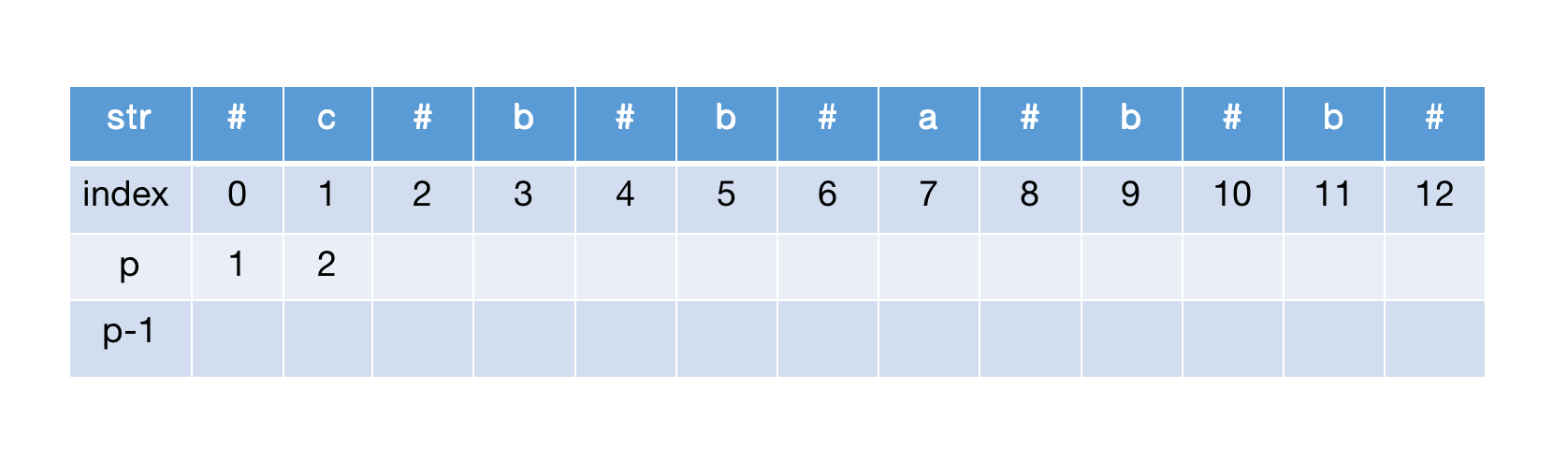
计算str[2],左右扩展后到达边界
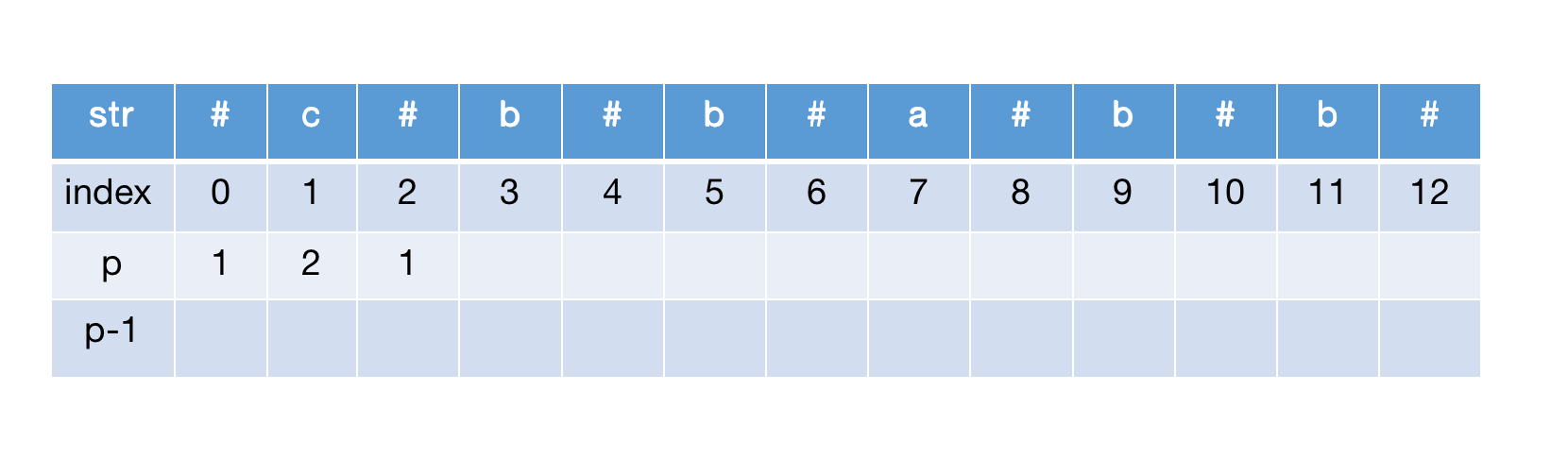
计算str[3],左右扩展匹配,半径加1,继续扩展到达边界
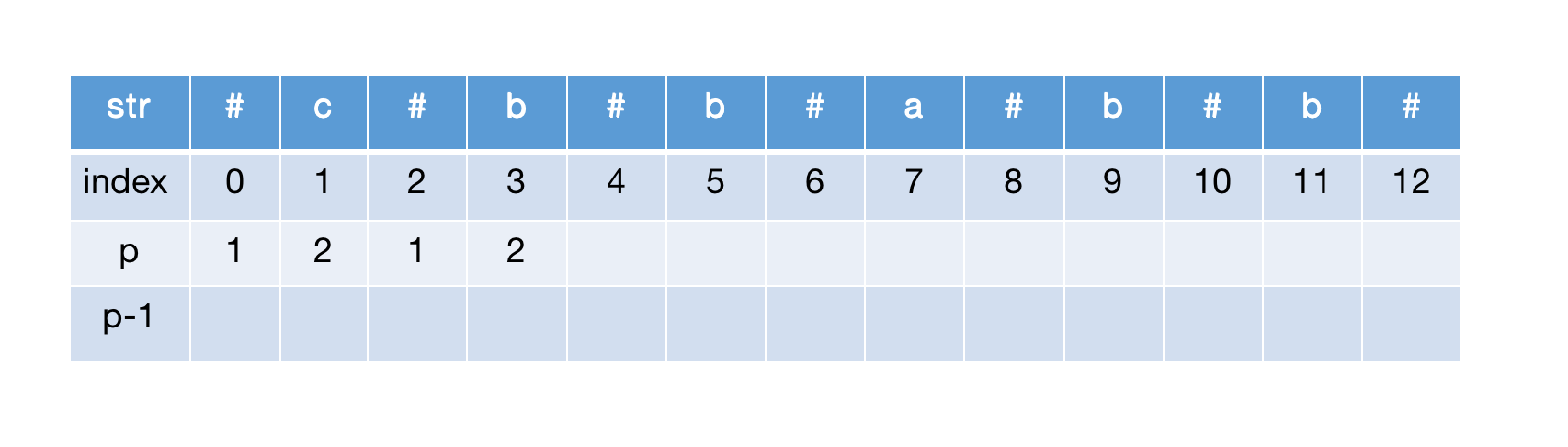
计算str[4],左右扩展匹配,半径加1,继续扩展匹配,加1,继续扩展到达边界
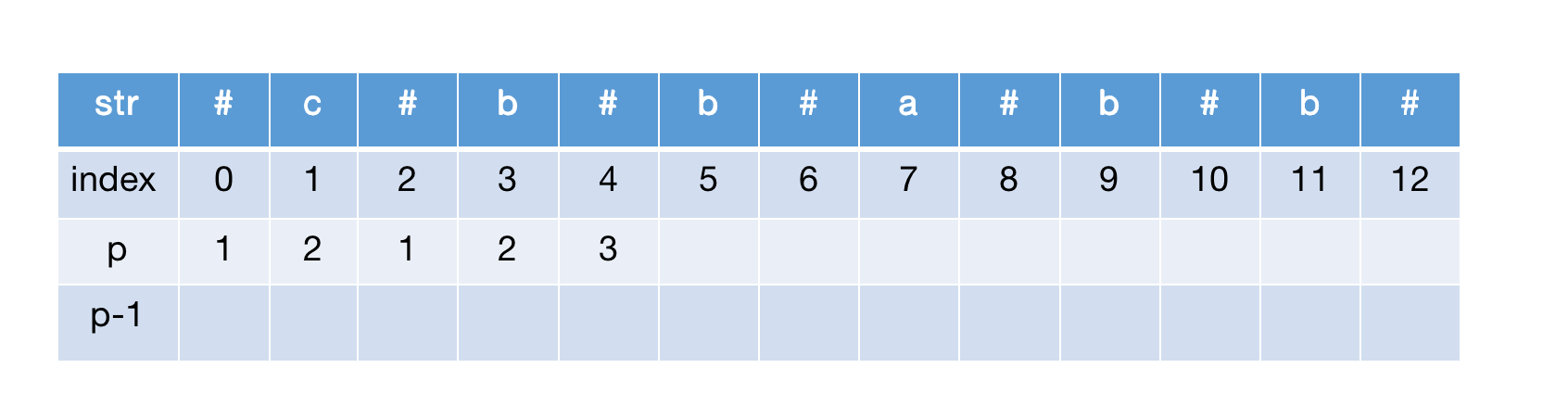
最终计算完的p数组:
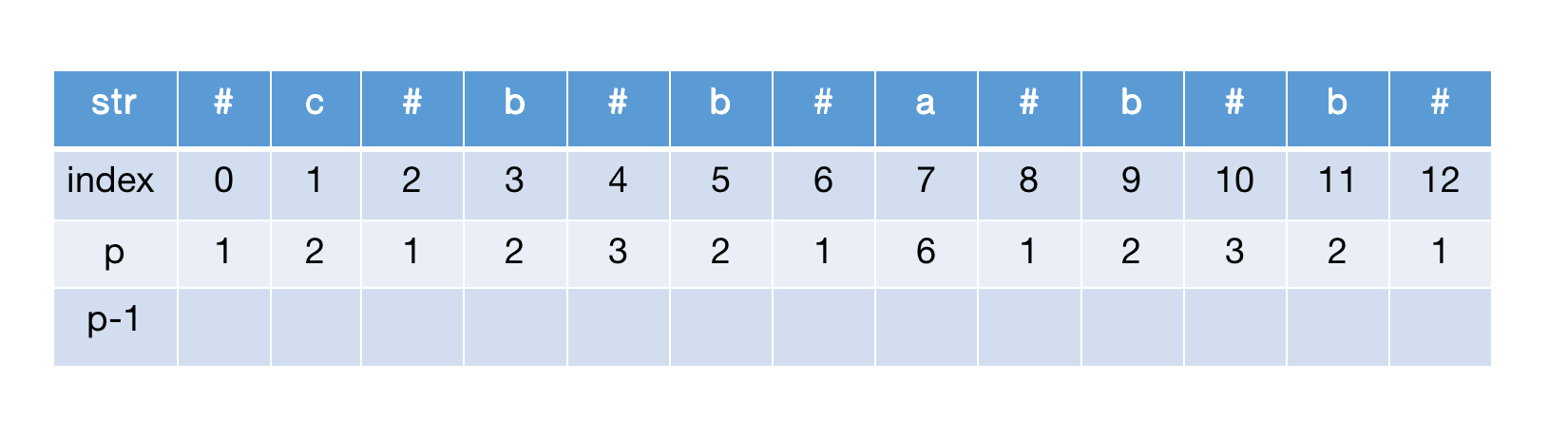
p-1数组
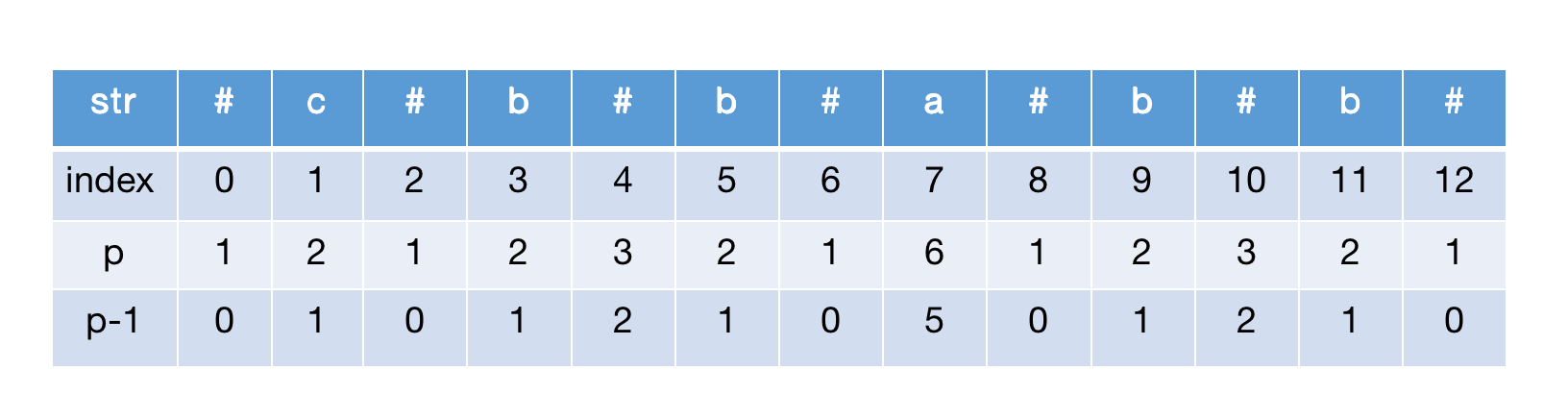
为什么还要p-1数组呢,这里简单分析下:
1.已知长度为n的回文串添加分隔符后长度为2n+1
2.假设上面计算的中心半径为p,那么容易得出2p-1 = 2n+1
3.通过2可以算出p = n+1 ===> p-1 = n,因此得到p-1数组即为回文串长度数组
第3步:如何在代码中计算p数组
以下图片为了方便理解把#符都省略掉
在第2步里介绍了马拉车算法核心在于复用回文串长度,在了解如何复用前先看下图:
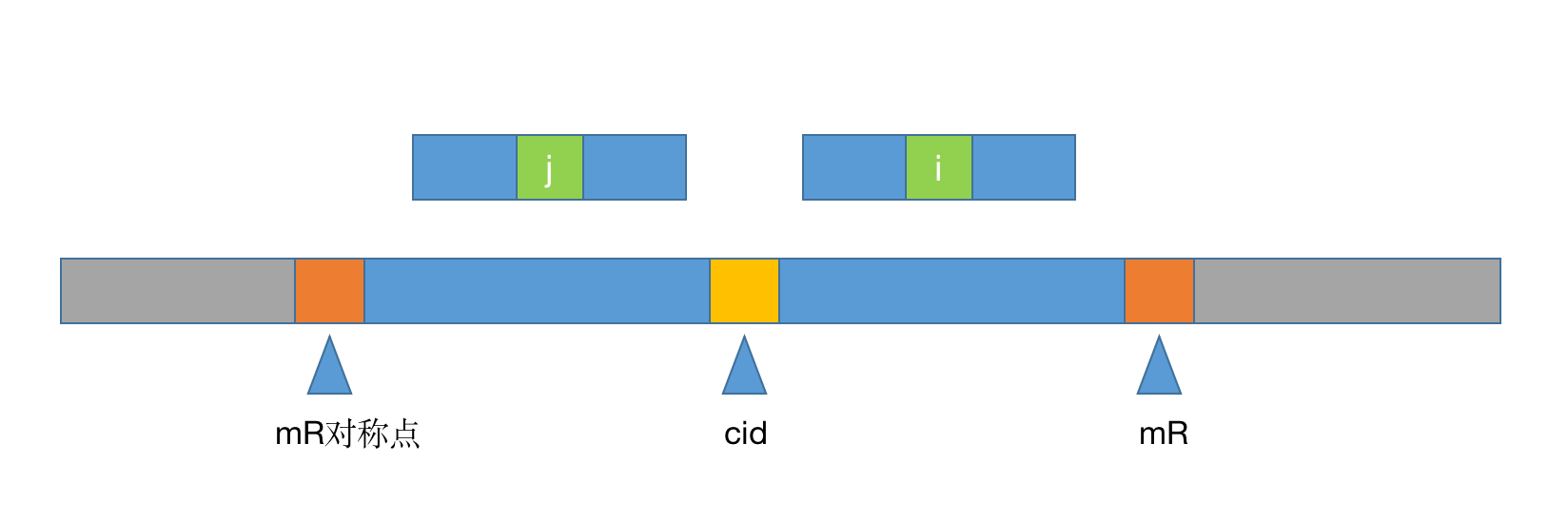
从上图容易获得三个关键信息:
i和j是关于cid中心对称的,容易得出j=2*cid - id的性质- 假设
mR为最长回文串的最右边界,那么容易得出cid+p[cid]-1 = mR - 假设以
i为中心的字符串也是回文串且长度不超过mR,那么根据上图可以得出i+p[i]-1<=mR
通过以上三个性质,先去计算最简单的一种情况: - 假如
i<mR,那么就可以考虑复用原则:
- 假如以
j为中心的回文串长度不超过cId的半径,那么p[i]=p[2*cid-j]是成立的,如下图:
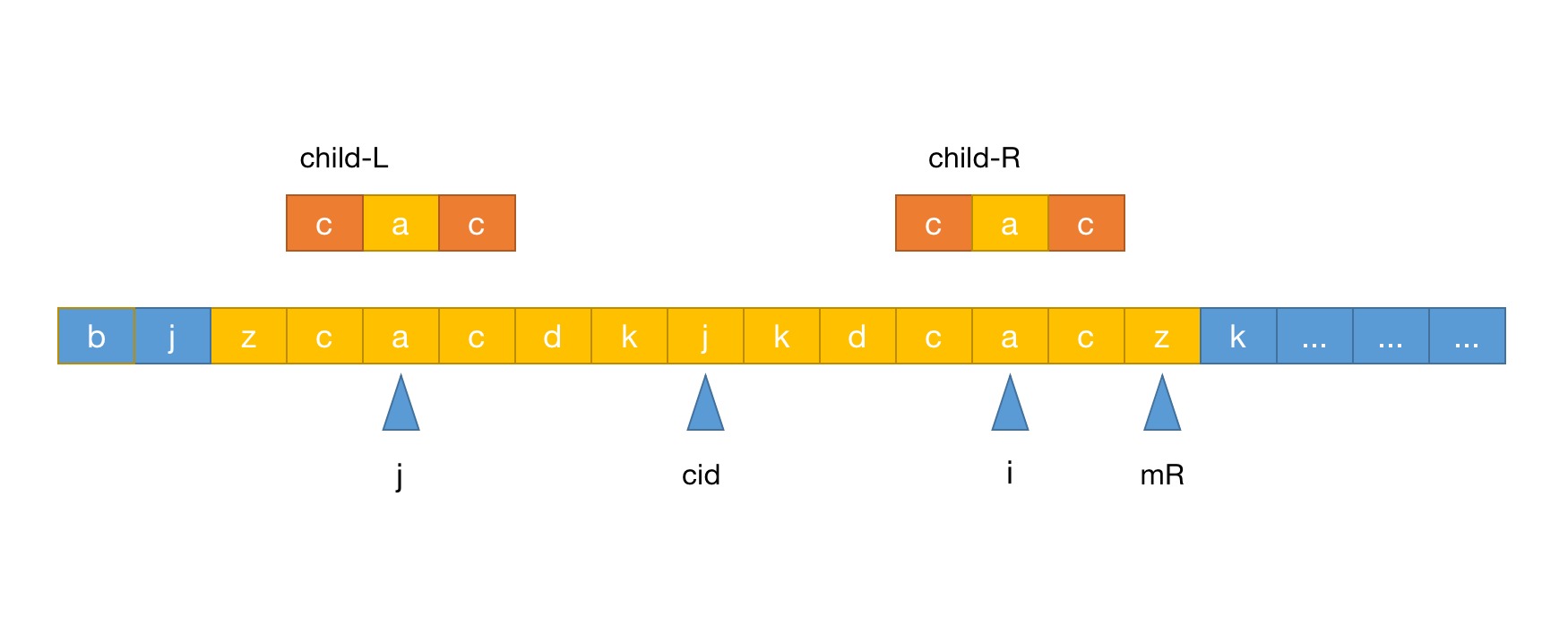
- 假如以
j为中心的回文串长度超过左边界,大概情况如下图:
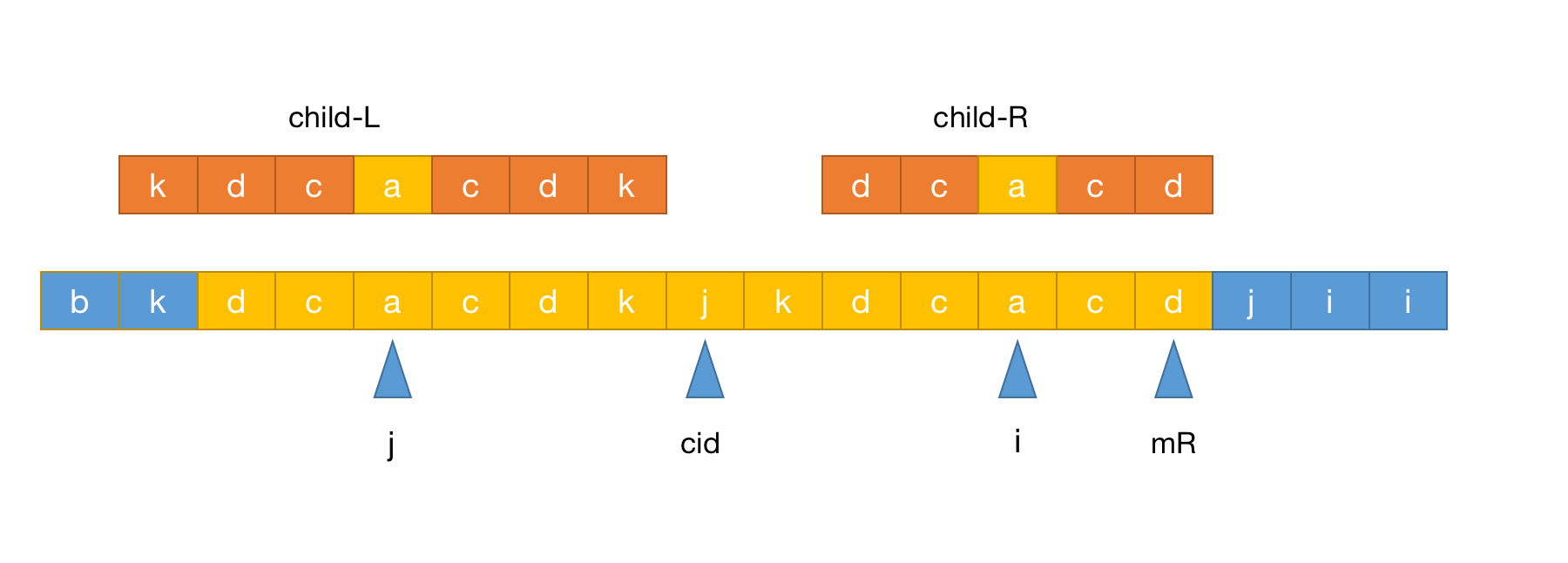
从上图可以看出j的半径明显要比i要大,因此p[i]=p[2*cid-j]明显不成立,但是由于j半径已经越过左边界,根据对称原则i的右边界可以到达右边界mR,也就是说可以得出p[i]=mR-i+1
- 假如以
- 假如
i>mR,这就简单了,赋值当前半径为1,继续使用中心扩展去左右扩展匹配 - 根据以上两点,总结出以下代码:
p[i] = i < mR ? Math.min(p[2 * cId - i], mR - i + 1) : 1; - 当计算完
p[i]后就要判断当前i的半径是否超过mR,超过则更新mR和cid
时间复杂度分析
为什么说Manacher的时间复杂度是O(n),下面可以分析下
假设字符串长度为n
首先把Manacher的核心代码提炼出来大概就是下面这段了
for (let i = 0; i < slen; i++) {
p[i] = i < mostR ? Math.min(p[2 * cId - i], mostR - i + 1) : 1;
while (i - p[i] >= 0 && i + p[i] < slen && str.charAt(i - p[i]) === str.charAt(i + p[i])) {
p[i]++
}
....
}
当i<mR:
- 当
p[mR-i+1]!=p[j]时,p[i]都是可以马上得到的,因为进入while循环后就会退出,时间复杂度是O(1),为什么是O(1),分两种情况讨论,如下:p[mR-i+1]>p[j]时,如下图:
这种情况p[j]小于p[mR-i+1],所以p[i]会直接取p[j]的值,进入while循环后也不会继续计算p[mR-i+1]<p[j],如下图:
而这种同理,虽然右子串childR到达mR,但是进入while循环就会退出,因为如果可以继续计算的话大概就是下面这样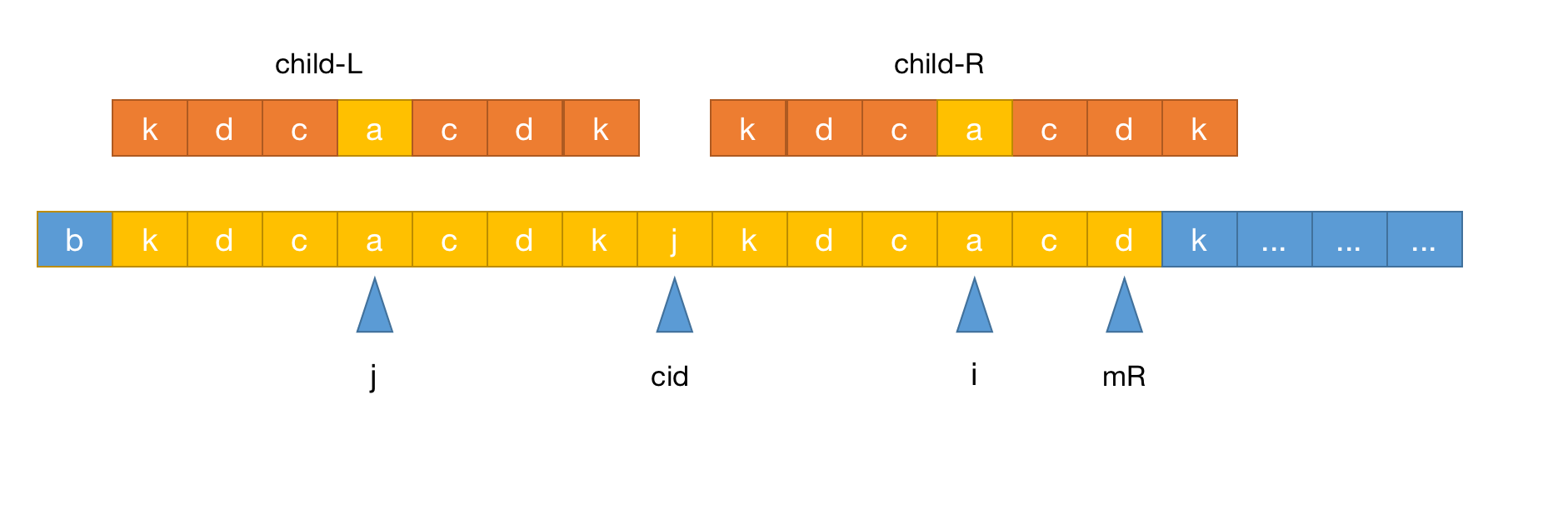
但其实这种情况是不可能出现的,因为这个时候mR早已是最右侧的k,也就是p[mR-i+1]=p[j]
- 当
p[mR-i+1]=p[j]时,进入while循环后会继续匹配,开始匹配的位置是str[i+p[i]]和str[i-p[i]],因为i+p[i]=mR+1,也就是匹配从mR的下一位开始,而匹配结束时停止的位置是mR',时间复杂度是O(mR'-mR)- 这里要注意当每次
i<mR&&p[mR-i+1]===p[j]时进入while循环,而mR是一直往后移动的,所以mR小于等于n,全部while循环加起来最多走过n次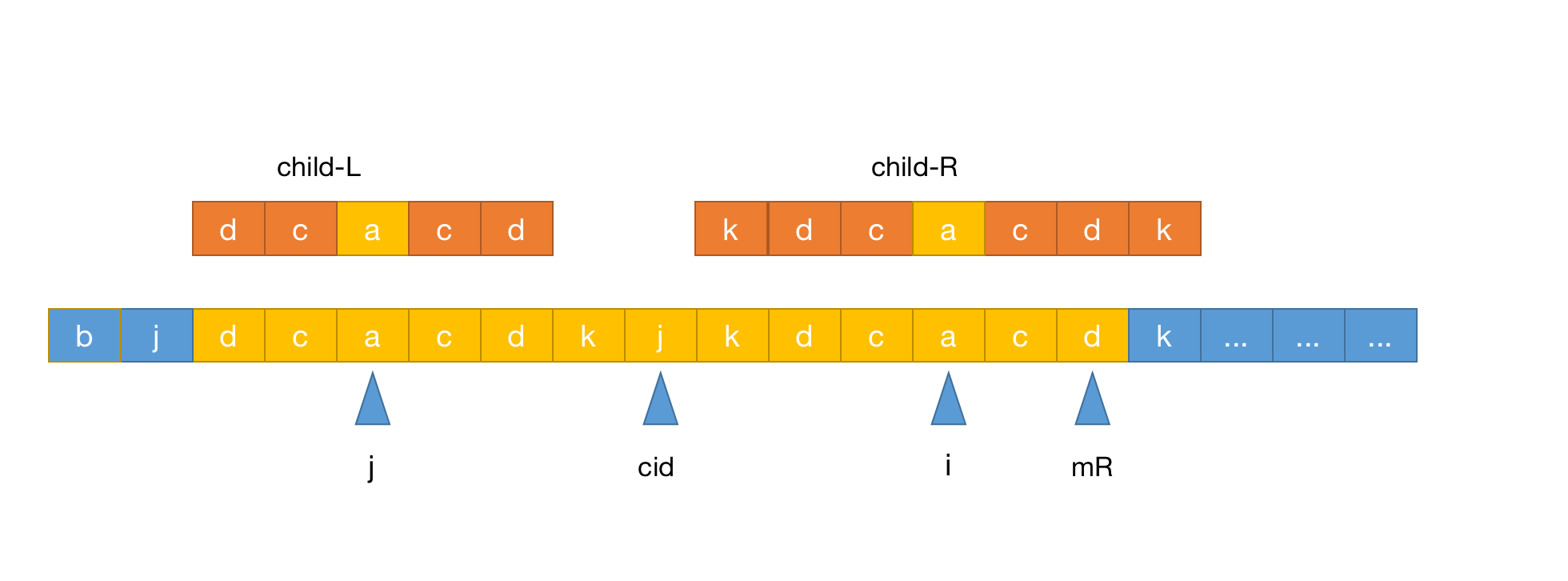
- 这里要注意当每次
当i>mR,直接进入while循环,同理最多全部循环最多n次,时间复杂度最大为O(n)
总结来说while循环是对mR进行扩展,如果说最长回文串到达N,那全部while循环加起来最多执行N次,因此Manacher算法时间复杂度为On
代码实现:中心扩展法
const longestPalindrome = (s) => {
if (s.length === 1) return s;
let start = 0, maxLen = 0;
const extendPalindrome = (s, l, r) => {
while (l >= 0 && r < s.length && s.charAt(l) === s.charAt(r)) {
l--;
r++;
}
if (maxLen < r - l - 1) {
start = l + 1;
maxLen = r - l - 1;
}
};
for (let i = 0; i < s.length - 1; i++) {
extendPalindrome(s, i, i);
extendPalindrome(s, i, i + 1)
}
return s.substring(start, start + maxLen)
};
代码实现:Manacher算法
const longestPalindrome = (s) => {
let str = '';
for (let i = 0; i < s.length; i++) {
str += `#${s.charAt(i)}`;
}
str += '#';
let slen = str.length,
p = Array(slen),
mostR = 0,
cId = 0,
palLen = 1,
palStr = s.substring(0, 1);
for (let i = 0; i < slen; i++) {
p[i] = i < mostR ? Math.min(p[2 * cId - i], mostR - i + 1) : 1;
while (i - p[i] >= 0 && i + p[i] < slen && str.charAt(i - p[i]) === str.charAt(i + p[i])) {
p[i]++
}
if (i + p[i] - 1 > mostR) {
mostR = i + p[i] - 1;
cId = i
}
if (p[i] - 1 > palLen) {
palLen = p[i] - 1;
palStr = str.substring(i - p[i] + 1, i + p[i]).replace(/#/g, '')
}
}
return palStr
};